Rosenau–Hyman equation

Last updated February 19, 2019

The Rosenau–Hyman equation or K(n,n) equation is a KdV-like equation having compacton solutions. This nonlinear partial differential equation is of the form^[1]

In mathematics, the Korteweg–de Vries (KdV) equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. KdV can be solved by means of the inverse scattering transform. The mathematical theory behind the KdV equation is a topic of active research. The KdV equation was first introduced by Boussinesq and rediscovered by Diederik Korteweg and Gustav de Vries (1895).

In the theory of integrable systems, a compacton, introduced in, is a soliton with compact support.

Partial differential equation differential equation that contains unknown multivariable functions and their partial derivatives

In mathematics, a partial differential equation (PDE) is a differential equation that contains beforehand unknown multivariable functions and their partial derivatives. PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a computer model. A special case is ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.

u_{t}+a(u^{n})_{x}+(u^{n})_{xxx}=0.\,

The equation is named after Philip Rosenau and James M. Hyman, who used in their 1993 study of compactons.^[2]

Philip Rosenau, is an Israeli mathematician and a poet. He is a Professor at the Department of Applied Mathematics at Tel Aviv University. He introduced compactons, along with James M. Hyman.

James Macklin "Mac" Hyman is an applied mathematician formerly at Los Alamos National Laboratory and currently at Tulane University in the United States. He received his undergraduate degree from Tulane University and his PhD in 1976 from NYU's Courant Institute of Mathematical Sciences under Peter Lax with thesis The method of lines solution of partial differential equations.

The K(n,n) equation has the following traveling wave solutions:

when a > 0

u(x,t)=\left({\frac {2cn}{a(n+1)}}\sin ^{2}\left({\frac {n-1}{2n}}{\sqrt {a}}(x-ct+b)\right)\right)^{1/(n-1)},

when a < 0

u(x,t)=\left({\frac {2cn}{a(n+1)}}\sinh ^{2}\left({\frac {n-1}{2n}}{\sqrt {-a}}(x-ct+b)\right)\right)^{1/(n-1)},

u(x,t)=\left({\frac {2cn}{a(n+1)}}\cosh ^{2}\left({\frac {n-1}{2n}}{\sqrt {-a}}(x-ct+b)\right)\right)^{1/(n-1)}.

Related Research Articles

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends.

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions.

In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any real number $x$ and integer $n$ it holds that

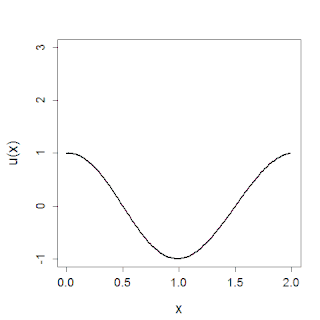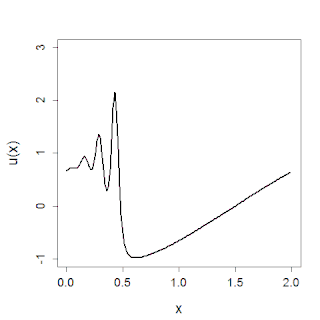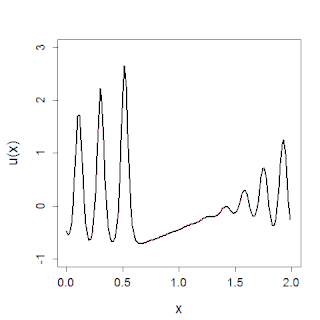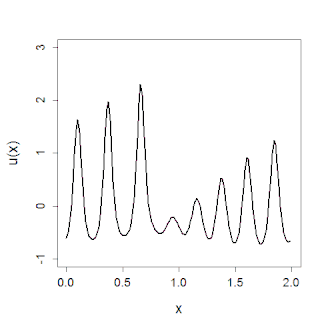
The sine-Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally introduced by Edmond Bour (1862) in the course of study of surfaces of constant negative curvature as the Gauss–Codazzi equation for surfaces of curvature −1 in 3-space, and rediscovered by Frenkel and Kontorova (1939) in their study of crystal dislocations known as the Frenkel–Kontorova model. This equation attracted a lot of attention in the 1970s due to the presence of soliton solutions.

In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. One may use the trigonometric identities to simplify certain integrals containing radical expressions:

Substitution 1. If the integrand contains a² − x², let
and use the identity

Substitution 2. If the integrand contains a² + x², let
and use the identity

Substitution 3. If the integrand contains x² − a², let
and use the identity

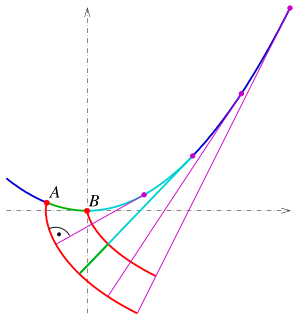
In the differential geometry of curves, an involute is a curve obtained from another given curve by one of two methods.

In physics, a breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even distribution of initially localized energy.

Universal Transverse Mercator coordinate system coordinate system

The Universal Transverse Mercator (UTM) conformal projection uses a 2-dimensional Cartesian coordinate system to give locations on the surface of the Earth. Like the traditional method of latitude and longitude, it is a horizontal position representation, i.e. it is used to identify locations on the Earth independently of altitude. However, it differs from that method in several respects.

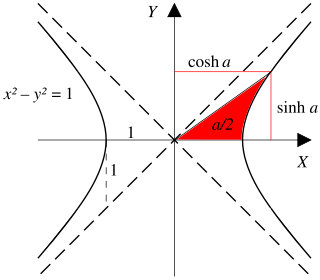
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions.

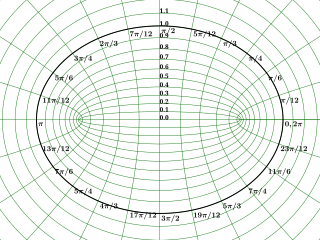
In geometry, the elliptic(al) coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci $and are generally taken to be fixed at and, respectively, on the -axis of the Cartesian coordinate system.$

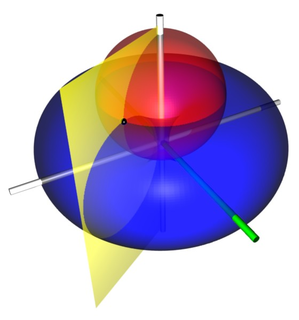
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci $and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.$

Elliptic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional elliptic coordinate system in the perpendicular $-direction. Hence, the coordinate surfaces are prisms of confocal ellipses and hyperbolae. The two foci and are generally taken to be fixed at and, respectively, on the -axis of the Cartesian coordinate system.$

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativisic velocity addition formula.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.

Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.

There are many ways to derive the Lorentz transformations utilizing a variety of physical principles, ranging from Maxwell's equations to Einstein's postulates of special relativity, and mathematical tools, spanning from elementary algebra and hyperbolic functions, to linear algebra and group theory.

The Frenkel–Kontorova model, also known as the FK model, is a fundamental model of low-dimensional nonlinear physics.

In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.

References

↑ Polyanin, Andrei D.; Zaitsev, Valentin F., Handbook of Nonlinear Partial Differential Equations (Second ed.), CRC Press, p. 891, ISBN 1584882972
↑ Rosenau, Philip; Hyman, James M. (1993), "Compactons: Solitons with finite wavelength", Physical Review Letters, American Physical Society, 70 (5): 564–567, Bibcode:1993PhRvL..70..564R, doi:10.1103/PhysRevLett.70.564, PMID 10054146

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Polyanin, Andrei D.; Zaitsev, Valentin F., Handbook of Nonlinear Partial Differential Equations (Second ed.), CRC Press, p. 891, ISBN 1584882972

[2] Rosenau, Philip; Hyman, James M. (1993), "Compactons: Solitons with finite wavelength", Physical Review Letters, American Physical Society, 70 (5): 564–567, Bibcode:1993PhRvL..70..564R, doi:10.1103/PhysRevLett.70.564, PMID 10054146