
Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into computer programs, to calculate the structures and properties of molecules, groups of molecules, and solids. The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion, achieving an accurate quantum mechanical depiction of chemical systems analytically, or in a closed form, is not feasible. The complexity inherent in many-body problem exacerbates the challenge of providing detailed descriptions in quantum mechanical systems. While computational results normally complement the information obtained by chemical experiments, it can in some cases predict unobserved chemical phenomena.

A generegulatory network (GRN) is a collection of molecular regulators that interact with each other and with other substances in the cell to govern the gene expression levels of mRNA and proteins which, in turn, determine the function of the cell. GRN also play a central role in morphogenesis, the creation of body structures, which in turn is central to evolutionary developmental biology (evo-devo).
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is different from chemical thermodynamics, which deals with the direction in which a reaction occurs but in itself tells nothing about its rate. Chemical kinetics includes investigations of how experimental conditions influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition states, as well as the construction of mathematical models that also can describe the characteristics of a chemical reaction.

Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determined by comparing their results to the real-world outcomes they aim to predict. Computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics, astrophysics, climatology, chemistry, biology and manufacturing, as well as human systems in economics, psychology, social science, health care and engineering. Simulation of a system is represented as the running of the system's model. It can be used to explore and gain new insights into new technology and to estimate the performance of systems too complex for analytical solutions.
Cooperativity is a phenomenon displayed by systems involving identical or near-identical elements, which act dependently of each other, relative to a hypothetical standard non-interacting system in which the individual elements are acting independently. One manifestation of this is enzymes or receptors that have multiple binding sites where the affinity of the binding sites for a ligand is apparently increased, positive cooperativity, or decreased, negative cooperativity, upon the binding of a ligand to a binding site. For example, when an oxygen atom binds to one of hemoglobin's four binding sites, the affinity to oxygen of the three remaining available binding sites increases; i.e. oxygen is more likely to bind to a hemoglobin bound to one oxygen than to an unbound hemoglobin. This is referred to as cooperative binding.
A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used, to distinguish over hybrid systems such as those that combine neural nets and fuzzy logic, or electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.
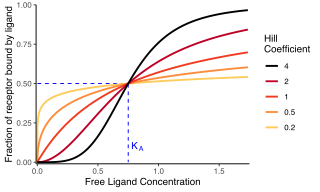
In biochemistry and pharmacology, the Hill equation refers to two closely related equations that reflect the binding of ligands to macromolecules, as a function of the ligand concentration. A ligand is "a substance that forms a complex with a biomolecule to serve a biological purpose", and a macromolecule is a very large molecule, such as a protein, with a complex structure of components. Protein-ligand binding typically changes the structure of the target protein, thereby changing its function in a cell.

In the field of molecular modeling, docking is a method which predicts the preferred orientation of one molecule to a second when a ligand and a target are bound to each other to form a stable complex. Knowledge of the preferred orientation in turn may be used to predict the strength of association or binding affinity between two molecules using, for example, scoring functions.

Enzyme kinetics is the study of the rates of enzyme-catalysed chemical reactions. In enzyme kinetics, the reaction rate is measured and the effects of varying the conditions of the reaction are investigated. Studying an enzyme's kinetics in this way can reveal the catalytic mechanism of this enzyme, its role in metabolism, how its activity is controlled, and how a drug or a modifier might affect the rate.
Metabolic network modelling, also known as metabolic network reconstruction or metabolic pathway analysis, allows for an in-depth insight into the molecular mechanisms of a particular organism. In particular, these models correlate the genome with molecular physiology. A reconstruction breaks down metabolic pathways into their respective reactions and enzymes, and analyzes them within the perspective of the entire network. In simplified terms, a reconstruction collects all of the relevant metabolic information of an organism and compiles it in a mathematical model. Validation and analysis of reconstructions can allow identification of key features of metabolism such as growth yield, resource distribution, network robustness, and gene essentiality. This knowledge can then be applied to create novel biotechnology.
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation system for which the reaction rates are known. It was created by Joseph L. Doob and others, presented by Dan Gillespie in 1976, and popularized in 1977 in a paper where he uses it to simulate chemical or biochemical systems of reactions efficiently and accurately using limited computational power. As computers have become faster, the algorithm has been used to simulate increasingly complex systems. The algorithm is particularly useful for simulating reactions within cells, where the number of reagents is low and keeping track of every single reaction is computationally feasible. Mathematically, it is a variant of a dynamic Monte Carlo method and similar to the kinetic Monte Carlo methods. It is used heavily in computational systems biology.
The Systems Biology Markup Language (SBML) is a representation format, based on XML, for communicating and storing computational models of biological processes. It is a free and open standard with widespread software support and a community of users and developers. SBML can represent many different classes of biological phenomena, including metabolic networks, cell signaling pathways, regulatory networks, infectious diseases, and many others. It has been proposed as a standard for representing computational models in systems biology today.

The Systems Biology Ontology (SBO) is a set of controlled, relational vocabularies of terms commonly used in systems biology, and in particular in computational modeling.
Systems immunology is a research field under systems biology that uses mathematical approaches and computational methods to examine the interactions within cellular and molecular networks of the immune system. The immune system has been thoroughly analyzed as regards to its components and function by using a "reductionist" approach, but its overall function can't be easily predicted by studying the characteristics of its isolated components because they strongly rely on the interactions among these numerous constituents. It focuses on in silico experiments rather than in vivo.

A cellular model is a mathematical model of aspects of a biological cell, for the purposes of in silico research.
Quantemol Ltd is based in University College London initiated by Professor Jonathan Tennyson FRS and Dr. Daniel Brown in 2004. The company initially developed a unique software tool, Quantemol-N, which provides full accessibility to the highly sophisticated UK molecular R-matrix codes, used to model electron polyatomic molecule interactions. Since then Quantemol has widened to further types of simulation, with plasmas and industrial plasma tools, in Quantemol-VT in 2013 and launched in 2016 a sustainable database Quantemol-DB, representing the chemical and radiative transport properties of a wide range of plasmas.
Virtual Cell (VCell) is an open-source software platform for modeling and simulation of living organisms, primarily cells. It has been designed to be a tool for a wide range of scientists, from experimental cell biologists to theoretical biophysicists.
Multi-state modeling of biomolecules refers to a series of techniques used to represent and compute the behaviour of biological molecules or complexes that can adopt a large number of possible functional states.
libRoadRunner is a C/C++ software library that supports simulation of SBML based models.. It uses LLVM to generate extremely high-performance code and is the fastest SBML-based simulator currently available. Its main purpose is for use as a reusable library that can be hosted by other applications, particularly on large compute clusters for doing parameter optimization where performance is critical. It also has a set of Python bindings that allow it to be easily used from Python.
Smoldyn is an open-source software application for cell-scale biochemical simulations. It uses particle-based simulation, meaning that it simulates each molecule of interest individually, in order to capture natural stochasticity and yield nanometer-scale spatial resolution. Simulated molecules diffuse, react, are confined by surfaces, and bind to membranes in similar manners as in real biochemical systems.









