An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron receives one or more inputs and sums them to produce an output. Usually, each input is separately weighted, and the sum is often added to a term known as a bias, before being passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. Non-monotonic, unbounded and oscillating activation functions with multiple zeros that outperform sigmoidal and ReLU-like activation functions on many tasks have also been recently explored. The thresholding function has inspired building logic gates referred to as threshold logic; applicable to building logic circuits resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in recent times.
Hebbian theory is a neuropsychological theory claiming that an increase in synaptic efficacy arises from a presynaptic cell's repeated and persistent stimulation of a postsynaptic cell. It is an attempt to explain synaptic plasticity, the adaptation of brain neurons during the learning process. It was introduced by Donald Hebb in his 1949 book The Organization of Behavior. The theory is also called Hebb's rule, Hebb's postulate, and cell assembly theory. Hebb states it as follows:
Let us assume that the persistence or repetition of a reverberatory activity tends to induce lasting cellular changes that add to its stability. ... When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
Neuromorphic computing is an approach to computing that is inspired by the structure and function of the human brain. A neuromorphic computer/chip is any device that uses physical artificial neurons to do computations. In recent times, the term neuromorphic has been used to describe analog, digital, mixed-mode analog/digital VLSI, and software systems that implement models of neural systems. The implementation of neuromorphic computing on the hardware level can be realized by oxide-based memristors, spintronic memories, threshold switches, transistors, among others. Training software-based neuromorphic systems of spiking neural networks can be achieved using error backpropagation, e.g., using Python based frameworks such as snnTorch, or using canonical learning rules from the biological learning literature, e.g., using BindsNet.

A neural circuit is a population of neurons interconnected by synapses to carry out a specific function when activated. Multiple neural circuits interconnect with one another to form large scale brain networks.
Bursting, or burst firing, is an extremely diverse general phenomenon of the activation patterns of neurons in the central nervous system and spinal cord where periods of rapid action potential spiking are followed by quiescent periods much longer than typical inter-spike intervals. Bursting is thought to be important in the operation of robust central pattern generators, the transmission of neural codes, and some neuropathologies such as epilepsy. The study of bursting both directly and in how it takes part in other neural phenomena has been very popular since the beginnings of cellular neuroscience and is closely tied to the fields of neural synchronization, neural coding, plasticity, and attention.
Computational neurogenetic modeling (CNGM) is concerned with the study and development of dynamic neuronal models for modeling brain functions with respect to genes and dynamic interactions between genes. These include neural network models and their integration with gene network models. This area brings together knowledge from various scientific disciplines, such as computer and information science, neuroscience and cognitive science, genetics and molecular biology, as well as engineering.
Oja's learning rule, or simply Oja's rule, named after Finnish computer scientist Erkki Oja, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time. It is a modification of the standard Hebb's Rule that, through multiplicative normalization, solves all stability problems and generates an algorithm for principal components analysis. This is a computational form of an effect which is believed to happen in biological neurons.

Spiking neural networks (SNNs) are artificial neural networks that more closely mimic natural neural networks. In addition to neuronal and synaptic state, SNNs incorporate the concept of time into their operating model. The idea is that neurons in the SNN do not transmit information at each propagation cycle, but rather transmit information only when a membrane potential—an intrinsic quality of the neuron related to its membrane electrical charge—reaches a specific value, called the threshold. When the membrane potential reaches the threshold, the neuron fires, and generates a signal that travels to other neurons which, in turn, increase or decrease their potentials in response to this signal. A neuron model that fires at the moment of threshold crossing is also called a spiking neuron model.
GENESIS is a simulation environment for constructing realistic models of neurobiological systems at many levels of scale including: sub-cellular processes, individual neurons, networks of neurons, and neuronal systems. These simulations are “computer-based implementations of models whose primary objective is to capture what is known of the anatomical structure and physiological characteristics of the neural system of interest”. GENESIS is intended to quantify the physical framework of the nervous system in a way that allows for easy understanding of the physical structure of the nerves in question. “At present only GENESIS allows parallelized modeling of single neurons and networks on multiple-instruction-multiple-data parallel computers.” Development of GENESIS software spread from its home at Caltech to labs at the University of Texas at San Antonio, the University of Antwerp, the National Centre for Biological Sciences in Bangalore, the University of Colorado, the Pittsburgh Supercomputing Center, the San Diego Supercomputer Center, and Emory University.
BCM theory, BCM synaptic modification, or the BCM rule, named for Elie Bienenstock, Leon Cooper, and Paul Munro, is a physical theory of learning in the visual cortex developed in 1981. The BCM model proposes a sliding threshold for long-term potentiation (LTP) or long-term depression (LTD) induction, and states that synaptic plasticity is stabilized by a dynamic adaptation of the time-averaged postsynaptic activity. According to the BCM model, when a pre-synaptic neuron fires, the post-synaptic neurons will tend to undergo LTP if it is in a high-activity state, or LTD if it is in a lower-activity state. This theory is often used to explain how cortical neurons can undergo both LTP or LTD depending on different conditioning stimulus protocols applied to pre-synaptic neurons.

Biological neuron models, also known as a spiking neuron models, are mathematical descriptions of neurons. In particular, these models describe how the voltage potential across the cell membrane changes over time. In an experimental setting, stimulating neurons with an electrical current generates an action potential, that propagates down the neuron's axon. This spike branches out to a large number of downstream neurons, where the signals terminate at synapses. As many as 85% of neurons in the neocortex, the outermost layer of the mammalian brain, consist of excitatory pyramidal neurons, and each pyramidal neuron receives tens of thousands of inputs from other neurons. Thus, spiking neurons are a major information processing unit of the nervous system.
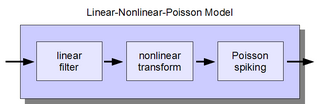
The linear-nonlinear-Poisson (LNP) cascade model is a simplified functional model of neural spike responses. It has been successfully used to describe the response characteristics of neurons in early sensory pathways, especially the visual system. The LNP model is generally implicit when using reverse correlation or the spike-triggered average to characterize neural responses with white-noise stimuli.
Brain simulation is the concept of creating a functioning computer model of a brain or part of a brain. Brain simulation projects intend to contribute to a complete understanding of the brain, and eventually also assist the process of treating and diagnosing brain diseases.
A Bayesian Confidence Propagation Neural Network (BCPNN) is an artificial neural network inspired by Bayes' theorem, which regards neural computation and processing as probabilistic inference. Neural unit activations represent probability ("confidence") in the presence of input features or categories, synaptic weights are based on estimated correlations and the spread of activation corresponds to calculating posterior probabilities. It was originally proposed by Anders Lansner and Örjan Ekeberg at KTH Royal Institute of Technology. This probabilistic neural network model can also be run in generative mode to produce spontaneous activations and temporal sequences.

NEST is a simulation software for spiking neural network models, including large-scale neuronal networks. NEST was initially developed by Markus Diesmann and Marc-Oliver Gewaltig and is now developed and maintained by the NEST Initiative.
An autapse is a chemical or electrical synapse from a neuron onto itself. It can also be described as a synapse formed by the axon of a neuron on its own dendrites, in vivo or in vitro.
The Tempotron is a supervised synaptic learning algorithm which is applied when the information is encoded in spatiotemporal spiking patterns. This is an advancement of the perceptron which does not incorporate a spike timing framework.
Channel sounding is a technique that evaluates a radio environment for wireless communication, especially MIMO systems. Because of the effect of terrain and obstacles, wireless signals propagate in multiple paths. To minimize or use the multipath effect, engineers use channel sounding to process the multidimensional spatial–temporal signal and estimate channel characteristics. This helps simulate and design wireless systems.
The Galves–Löcherbach model is a mathematical model for a network of neurons with intrinsic stochasticity.

Synthetic Nervous System (SNS) is a computational neuroscience model that may be developed with the Functional Subnetwork Approach (FSA) to create biologically plausible models of circuits in a nervous system. The FSA enables the direct analytical tuning of dynamical networks that perform specific operations within the nervous system without the need for global optimization methods like genetic algorithms and reinforcement learning. The primary use case for a SNS is system control, where the system is most often a simulated biomechanical model or a physical robotic platform. An SNS is a form of a neural network much like artificial neural networks (ANNs), convolutional neural networks (CNN), and recurrent neural networks (RNN). The building blocks for each of these neural networks is a series of nodes and connections denoted as neurons and synapses. More conventional artificial neural networks rely on training phases where they use large data sets to form correlations and thus “learn” to identify a given object or pattern. When done properly this training results in systems that can produce a desired result, sometimes with impressive accuracy. However, the systems themselves are typically “black boxes” meaning there is no readily distinguishable mapping between structure and function of the network. This makes it difficult to alter the function, without simply starting over, or extract biological meaning except in specialized cases. The SNS method differentiates itself by using details of both structure and function of biological nervous systems. The neurons and synapse connections are intentionally designed rather than iteratively changed as part of a learning algorithm.















