
An abacus, also called a counting frame, is a hand-operated calculating tool which was used from ancient times in the ancient Near East, Europe, China, and Russia, until the adoption of the Arabic numeral system. An abacus consists of a two-dimensional array of slidable beads. In their earliest designs, the beads could be loose on a flat surface or sliding in grooves. Later the beads were made to slide on rods and built into a frame, allowing faster manipulation.

The Battle of Salamis was a naval battle fought in 480 BC, between an alliance of Greek city-states under Themistocles, and the Achaemenid Empire under King Xerxes. It resulted in a victory for the outnumbered Greeks. The battle was fought in the straits between the mainland and Salamis, an island in the Saronic Gulf near Athens, and marked the high point of the second Persian invasion of Greece. It was arguably the largest naval battle of the ancient world, and marked a turning point in the invasion.

Boustrophedon is a style of writing in which alternate lines of writing are reversed, with letters also written in reverse, mirror-style. This is in contrast to modern European languages, where lines always begin on the same side, usually the left.

The Battle of Mycale was one of the two major battles that ended the second Persian invasion of Greece during the Greco-Persian Wars. It took place on or about August 27, 479 BC on the slopes of Mount Mycale, on the coast of Ionia, opposite the island of Samos. The battle was fought between an alliance of the Greek city-states, including Sparta, Athens and Corinth, and the Persian Empire of Xerxes I.
A calculation is a deliberate mathematical process that transforms one or more inputs into one or more outputs or results. The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm, to the vague heuristics of calculating a strategy in a competition, or calculating the chance of a successful relationship between two people.
A numerical digit or numeral is a single symbol used alone or in combinations, to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits of the hands correspond to the ten symbols of the common base 10 numeral system, i.e. the decimal digits.

The Battle of Artemisium or Artemision was a series of naval engagements over three days during the second Persian invasion of Greece. The battle took place simultaneously with the land battle at Thermopylae, in August or September 480 BC, off the coast of Euboea and was fought between an alliance of Greek city-states, including Sparta, Athens, Corinth and others, and the Persian Empire of Xerxes I.

The Battle of Plataea was the final land battle during the second Persian invasion of Greece. It took place in 479 BC near the city of Plataea in Boeotia, and was fought between an alliance of the Greek city-states, and the Achaemenid Empire of Xerxes I.

The Ancient Romans developed the Roman hand abacus, a portable, but less capable, base-10 version of earlier abacuses like those that were used by the Greeks and Babylonians.
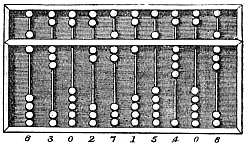
The suanpan, also spelled suan pan or souanpan) is an abacus of Chinese origin, earliest first known written documentation of the Chinese abacus dates to the 2nd century BCE during the Han dynasty, and later, described in a 190 CE book of the Eastern Han dynasty, namely Supplementary Notes on the Art of Figures written by Xu Yue. However, the exact design of this suanpan is not known. Usually, a suanpan is about 20 cm (8 in) tall and it comes in various widths depending on the application. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads on each rod in the bottom deck. The beads are usually rounded and made of a hardwood. The beads are counted by moving them up or down towards the beam. The suanpan can be reset to the starting position instantly by a quick jerk around the horizontal axis to spin all the beads away from the horizontal beam at the center.
Location arithmetic is the additive (non-positional) binary numeral systems, which John Napier explored as a computation technique in his treatise Rabdology (1617), both symbolically and on a chessboard-like grid.

Jetons or jettons are tokens or coin-like medals produced across Europe from the 13th through the 18th centuries. They were produced as counters for use in calculation on a counting board, a lined board similar to an abacus. Jetons for calculation were commonly used in Europe from about 1200 to 1700, and remained in occasional use into the early nineteenth century. They also found use as a money substitute in games, similar to modern casino chips or poker chips.

The Decree of Themistocles or Troezen Inscription is an ancient Greek inscription, found at Troezen, discussing Greek strategy in the Greco-Persian Wars, purported to have been issued by the Athenian assembly under the guidance of Themistocles. Since the publication of its contents in 1960, the authenticity of the decree has been the subject of much academic debate. The decree contradicted modern scholarly interpretations of Herodotus's account of the evacuation of Attica in 480 BC, in which it is stated that the evacuation was an emergency measure taken only after the Peloponnesian army failed to advance into Boeotia to fight the Persians. If the decree is authentic, the abandonment of Attica was part of a considered strategy aiming to draw the Persians into naval combat at Artemisium or Salamis.
Number systems have progressed from the use of fingers and tally marks, perhaps more than 40,000 years ago, to the use of sets of glyphs able to represent any conceivable number efficiently. The earliest known unambiguous notations for numbers emerged in Mesopotamia about 5000 or 6000 years ago.
A numeral is a character that denotes a number. The decimal number digits 0–9 are used widely in various writing systems throughout the world, however the graphemes representing the decimal digits differ widely. Therefore Unicode includes 22 different sets of graphemes for the decimal digits, and also various decimal points, thousands separators, negative signs, etc. Unicode also includes several non-decimal numerals such as Aegean numerals, Roman numerals, counting rod numerals, Mayan numerals, Cuneiform numerals and ancient Greek numerals. There is also a large number of typographical variations of the Western Arabic numerals provided for specialized mathematical use and for compatibility with earlier character sets, such as ² or ②, and composite characters such as ½.

Counting in prehistory was first assisted by using body parts, primarily the fingers. This is reflected in the etymology of certain number names, such as in the names of ten and hundred in the Proto-Indo-European numerals, both containing the root *dḱ also seen in the word for "finger".

The counting board is the precursor of the abacus, and the earliest known form of a counting device. Counting boards were made of stone or wood, and the counting was done on the board with beads, pebbles etc. Not many boards survive because of the perishable materials used in their construction, or the impossibility to identify the object as a counting board.The counting board was invented to facilitate and streamline numerical calculations in ancient civilizations. Its inception addressed the need for a practical tool to perform arithmetic operations efficiently. By using counters or tokens on a board with designated sections, people could easily keep track of quantities, trade, and financial transactions. This invention not only enhanced accuracy but also fueled the development of more sophisticated mathematical concepts and systems throughout history.
A timeline of numerals and arithmetic.
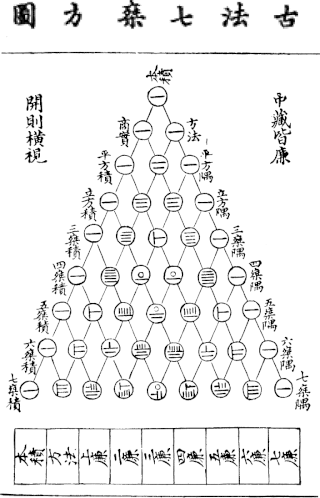
Counting rods (筭) are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.

The Darius Vase is a famous vase painted by an anonymous Magna Graecia Apulian vase painter, commonly called the Darius Painter, the most eminent representative at the end of the "Ornate Style" in South Italian red-figure vase painting. The vase was produced between 340 and 320 BCE, probably in a large factory-like workshop in the Greek city of Taranto, Magna Graecia, well before the fall of Taranto to the Romans in 272 BCE. It is an important work of Apulian vase painting.














