 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages)
|
The science of value, or value science, is a creation of philosopher Robert S. Hartman, which attempts to formally elucidate value theory using both formal and symbolic logic.
The fundamental principle, which functions as an axiom, and can be stated in symbolic logic, is that a thing is good insofar as it exemplifies its concept. To put it another way, "a thing is good if it has all its descriptive properties." This means, according to Hartman, that the good thing has a name, that the name has a meaning defined by a set of properties, and that the thing possesses all of the properties in the set. A thing is bad if it does not fulfill its description. If it doesn't fulfill its definition it is terrible (awful, miserable). A car, by definition, has brakes. A car which accelerates when the brakes are applied is an awful car, since a car by definition must have brakes. A horse, if we called it a car, would be an even worse car, with fewer of the properties of a car. The name we put on things is very important: it sets the norm for how we judge them.
He introduces three basic dimensions of value, systemic , extrinsic and intrinsic for sets of properties—perfection is to systemic value what goodness is to extrinsic value and what uniqueness is to intrinsic value—each with their own cardinality: finite, and . In practice, the terms "good" and "bad" apply to finite sets of properties, since this is the only case where there is a ratio between the total number of desired properties and the number of such properties possessed by some object being valued. (In the case where the number of properties is countably infinite, the extrinsic dimension of value, the exposition as well as the mere definition of a specific concept is taken into consideration.)
Hartman quantifies this notion by the principle that each property of the thing is worth as much as each other property, depending on the level of abstraction. [1] Hence, if a thing has n properties, each of them—if on the same level of abstraction—is proportionally worth n−1. . In other words, a car having brakes or having a gas cap are weighted equally so far as their value goes, so long as both are a part of one's definition of a "car." Since a gas cap is not normally a part of a car's definition, it would be given no weight. Headlights could be weighed twice, once or not at all depending on how headlights appear in the description of a car. Given a finite set of n properties, a thing is good if it is perceived to have all of the properties, fair if it has more than n/2 of them, average if n/2 of them, and bad if it has fewer than n/2.
Hartman goes on to consider infinite sets of properties. Hartman claims that according to a theorem of transfinite mathematics, any collection of material objects is at most denumerably infinite. [2] This is not, in fact, a theorem of mathematics. But, according to Hartman, people are capable of a denumerably infinite set of predicates, intended in as many ways, which he gives as . As this yields a notional cardinality of the continuum, Hartman advises that when setting out to describe a person, a continuum of properties would be most fitting and appropriate to bear in mind. This is the cardinality of intrinsic value in Hartman's system.
Although they play no role in ordinary mathematics, Hartman deploys the notion of aleph number reciprocals, as a sort of infinitesimal proportion. This, he contends goes to zero in the limit as the uncountable cardinals become larger. In Hartman's calculus, for example, the assurance in a Dear John letter, that "we will always be friends" has axiological value , whereas taking a metaphor literally would be slightly preferable, the reification having a value of .
Axiology is the philosophical study of value. It includes questions about the nature and classification of values and about what kinds of things have value. It is intimately connected with various other philosophical fields that crucially depend on the notion of value, like ethics, aesthetics or philosophy of religion. It is also closely related to value theory and meta-ethics. The term was first used by Eduard von Hartmann in 1887 and by Paul Lapie in 1902.
In mathematics, specifically set theory, the continuum hypothesis is a hypothesis about the possible sizes of infinite sets. It states that
there is no set whose cardinality is strictly between that of the integers and the real numbers,
In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case of infinite sets, the infinite cardinal numbers have been introduced, which are often denoted with the Hebrew letter (aleph) marked with subscript indicating their rank among the infinite cardinals.
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set contains 3 elements, and therefore has a cardinality of 3. Beginning in the late 19th century, this concept was generalized to infinite sets, which allows one to distinguish between different types of infinity, and to perform arithmetic on them. There are two approaches to cardinality: one which compares sets directly using bijections and injections, and another which uses cardinal numbers. The cardinality of a set may also be called its size, when no confusion with other notions of size is possible.
In mathematics, especially in order theory, the cofinality cf(A) of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A.
In mathematics, hyperreal numbers are an extension of the real numbers to include certain classes of infinite and infinitesimal numbers. A hyperreal number is said to be finite if, and only if, for some integer . is said to be infinitesimal if, and only if, for all integers . The term "hyper-real" was introduced by Edwin Hewitt in 1948.
In mathematics, transfinite numbers or infinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets. The term transfinite was coined in 1895 by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite. Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term transfinite also remains in use.
In mathematics, particularly in set theory, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets that can be well-ordered. They were introduced by the mathematician Georg Cantor and are named after the symbol he used to denote them, the Hebrew letter aleph (ℵ).
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. More explicitly, this means that is a regular cardinal if and only if every unbounded subset has cardinality . Infinite well-ordered cardinals that are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
In mathematics, particularly in set theory, the beth numbers are a certain sequence of infinite cardinal numbers, conventionally written , where is the Hebrew letter beth. The beth numbers are related to the aleph numbers, but unless the generalized continuum hypothesis is true, there are numbers indexed by that are not indexed by .
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.
In set theory, the cardinality of the continuum is the cardinality or "size" of the set of real numbers , sometimes called the continuum. It is an infinite cardinal number and is denoted by or .
Robert Schirokauer Hartman was a German-American logician and philosopher. His primary field of study was scientific axiology and he is known as its original theorist. His axiology is the basis of the Hartman Value Inventory (also known as the "Hartman Value Profile ", which is used in psychology to measure the character of an individual.
James Earl Baumgartner was an American mathematician who worked in set theory, mathematical logic and foundations, and topology.
The Vaught conjecture is a conjecture in the mathematical field of model theory originally proposed by Robert Lawson Vaught in 1961. It states that the number of countable models of a first-order complete theory in a countable language is finite or ℵ0 or 2ℵ0. Morley showed that the number of countable models is finite or ℵ0 or ℵ1 or 2ℵ0, which solves the conjecture except for the case of ℵ1 models when the continuum hypothesis fails. For this remaining case, Robin Knight has announced a counterexample to the Vaught conjecture and the topological Vaught conjecture. As of 2021, the counterexample has not been verified.
In mathematics, infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. Some of the things studied include continuous graphs and trees, extensions of Ramsey's theorem, and Martin's axiom. Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.
Infinity is something which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
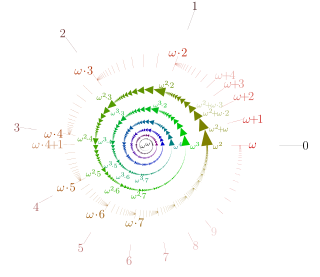
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
Lars Svenonius was a Swedish logician and philosopher.
In the mathematical discipline of set theory, a cardinal characteristic of the continuum is an infinite cardinal number that may consistently lie strictly between , and the cardinality of the continuum, that is, the cardinality of the set of all real numbers. The latter cardinal is denoted or . A variety of such cardinal characteristics arise naturally, and much work has been done in determining what relations between them are provable, and constructing models of set theory for various consistent configurations of them.
