Knowledge representation and reasoning is the field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can utilize to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology about how humans solve problems and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning, such as the application of rules or the relations of sets and subsets.
Description logics (DL) are a family of formal knowledge representation languages. Many DLs are more expressive than propositional logic but less expressive than first-order logic. In contrast to the latter, the core reasoning problems for DLs are (usually) decidable, and efficient decision procedures have been designed and implemented for these problems. There are general, spatial, temporal, spatiotemporal, and fuzzy description logics, and each description logic features a different balance between expressive power and reasoning complexity by supporting different sets of mathematical constructors.
The Web Ontology Language (OWL) is a family of knowledge representation languages for authoring ontologies. Ontologies are a formal way to describe taxonomies and classification networks, essentially defining the structure of knowledge for various domains: the nouns representing classes of objects and the verbs representing relations between the objects.

Decision tables are a concise visual representation for specifying which actions to perform depending on given conditions. They are algorithms whose output is a set of actions. The information expressed in decision tables could also be represented as decision trees or in a programming language as a series of if-then-else and switch-case statements.

Object-role modeling (ORM) is used to model the semantics of a universe of discourse. ORM is often used for data modeling and software engineering.
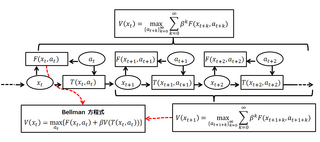
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality” prescribes.
Answer set programming (ASP) is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers—programs for generating stable models—are used to perform search. The computational process employed in the design of many answer set solvers is an enhancement of the DPLL algorithm and, in principle, it always terminates.
In philosophical logic, the concept of an impossible world is used to model certain phenomena that cannot be adequately handled using ordinary possible worlds. An impossible world, w, is the same sort of thing as a possible world , except that it is in some sense "impossible." Depending on the context, this may mean that some contradictions are true at w, that the normal laws of logic or of metaphysics fail to hold at w, or both.
Semantic integration is the process of interrelating information from diverse sources, for example calendars and to do lists, email archives, presence information, documents of all sorts, contacts, search results, and advertising and marketing relevance derived from them. In this regard, semantics focuses on the organization of and action upon information by acting as an intermediary between heterogeneous data sources, which may conflict not only by structure but also context or value.
Ontology alignment, or ontology matching, is the process of determining correspondences between concepts in ontologies. A set of correspondences is also called an alignment. The phrase takes on a slightly different meaning, in computer science, cognitive science or philosophy.

An autoencoder is a type of artificial neural network used to learn efficient codings of unlabeled data. The encoding is validated and refined by attempting to regenerate the input from the encoding. The autoencoder learns a representation (encoding) for a set of data, typically for dimensionality reduction, by training the network to ignore insignificant data (“noise”).
Frames are an artificial intelligence data structure used to divide knowledge into substructures by representing "stereotyped situations". They were proposed by Marvin Minsky in his 1974 article "A Framework for Representing Knowledge". Frames are the primary data structure used in artificial intelligence frame language; they are stored as ontologies of sets.
DOGMA, short for Developing Ontology-Grounded Methods and Applications, is the name of research project in progress at Vrije Universiteit Brussel's STARLab, Semantics Technology and Applications Research Laboratory. It is an internally funded project, concerned with the more general aspects of extracting, storing, representing and browsing information.
The dominance-based rough set approach (DRSA) is an extension of rough set theory for multi-criteria decision analysis (MCDA), introduced by Greco, Matarazzo and Słowiński. The main change compared to the classical rough sets is the substitution for the indiscernibility relation by a dominance relation, which permits one to deal with inconsistencies typical to consideration of criteria and preference-ordered decision classes.
Business Semantics Management (BSM) encompasses the technology, methodology, organization, and culture that brings business stakeholders together to collaboratively realize the reconciliation of their heterogeneous metadata; and consequently the application of the derived business semantics patterns to establish semantic alignment between the underlying data structures.

In computer science, information science and systems engineering, ontology engineering is a field which studies the methods and methodologies for building ontologies, which encompasses a representation, formal naming and definition of the categories, properties and relations between the concepts, data and entities. In a broader sense, this field also includes a knowledge construction of the domain using formal ontology representations such as OWL/RDF. A large-scale representation of abstract concepts such as actions, time, physical objects and beliefs would be an example of ontological engineering. Ontology engineering is one of the areas of applied ontology, and can be seen as an application of philosophical ontology. Core ideas and objectives of ontology engineering are also central in conceptual modeling.
Jan Vanthienen is a Belgian Information systems scientist and Professor of Information systems engineering at Leuven University, known for his contributions to Business Process Modeling, Process mining and Business Engineering.
Knowledge extraction is the creation of knowledge from structured and unstructured sources. The resulting knowledge needs to be in a machine-readable and machine-interpretable format and must represent knowledge in a manner that facilitates inferencing. Although it is methodically similar to information extraction (NLP) and ETL, the main criteria is that the extraction result goes beyond the creation of structured information or the transformation into a relational schema. It requires either the reuse of existing formal knowledge or the generation of a schema based on the source data.
In information technology a reasoning system is a software system that generates conclusions from available knowledge using logical techniques such as deduction and induction. Reasoning systems play an important role in the implementation of artificial intelligence and knowledge-based systems.

In information science a conceptualization is an abstract simplified view of some selected part of the world, containing the objects, concepts, and other entities that are presumed of interest for some particular purpose and the relationships between them. An explicit specification of a conceptualization is an ontology, and it may occur that a conceptualization can be realized by several distinct ontologies. An ontological commitment in describing ontological comparisons is taken to refer to that subset of elements of an ontology shared with all the others. "An ontology is language-dependent", its objects and interrelations described within the language it uses, while a conceptualization is always the same, more general, its concepts existing "independently of the language used to describe it". The relation between these terms is shown in the figure to the right.












