In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.
The fundamental theorem of algebra also known as d'Alembert's theorem or the d'Alembert-Gauss theorem states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.
In mathematics, the Weil conjectures were highly influential proposals by André Weil (1949). They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.
In complex analysis, de Branges's theorem, or the Bieberbach conjecture, is a theorem that gives a necessary condition on a holomorphic function in order for it to map the open unit disk of the complex plane injectively to the complex plane. It was posed by Ludwig Bieberbach (1916) and finally proven by Louis de Branges (1985).

In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers A with positive natural density contains a k-term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.
In geometric group theory, Gromov's theorem on groups of polynomial growth, first proved by Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index.

Terence "Terry" Chi-Shen Tao is an Australian-American mathematician. He is a professor of mathematics at the University of California, Los Angeles (UCLA), where he holds the James and Carol Collins chair. His research includes topics in harmonic analysis, partial differential equations, algebraic combinatorics, arithmetic combinatorics, geometric combinatorics, probability theory, compressed sensing and analytic number theory.

Transcendental number theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.

Ben Joseph Green FRS is a British mathematician, specialising in combinatorics and number theory. He is the Waynflete Professor of Pure Mathematics at the University of Oxford.
In number theory, the Green–Tao theorem, proved by Ben Green and Terence Tao in 2004, states that the sequence of prime numbers contains arbitrarily long arithmetic progressions. In other words, for every natural number k, there exist arithmetic progressions of primes with k terms. The proof is an extension of Szemerédi's theorem. The problem can be traced back to investigations of Lagrange and Waring from around 1770.

In mathematics, the Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.
In mathematics, in the field of additive combinatorics, a Gowers norm or uniformity norm is a class of norms on functions on a finite group or group-like object which quantify the amount of structure present, or conversely, the amount of randomness. They are used in the study of arithmetic progressions in the group. They are named after Timothy Gowers, who introduced it in his work on Szemerédi's theorem.

Julius Bogdan Borcea was a Romanian Swedish mathematician. His scientific work included vertex operator algebra and zero distribution of polynomials and entire functions, via correlation inequalities and statistical mechanics.

Alexander Nikolaevich Varchenko is a Soviet and Russian mathematician working in geometry, topology, combinatorics and mathematical physics.

Tamar Debora Ziegler is an Israeli mathematician known for her work in ergodic theory, combinatorics and number theory. She holds the Henry and Manya Noskwith Chair of Mathematics at the Einstein Institute of Mathematics at the Hebrew University.
Bernstein's theorem is an inequality relating the maximum modulus of a complex polynomial function on the unit disk with the maximum modulus of its derivative on the unit disk. It was proven by Sergei Bernstein while he was working on approximation theory.
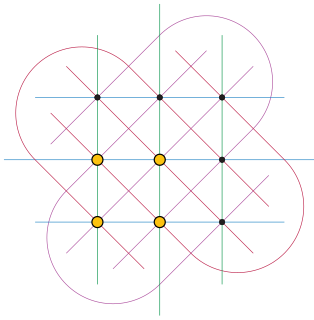
In affine geometry, a cap set is a subset of with no three elements in a line. The cap set problem is the problem of finding the size of the largest possible cap set, as a function of . The first few cap set sizes are 1, 2, 4, 9, 20, 45, 112, ....
In mathematics, the mean value problem was posed by Stephen Smale in 1981. This problem is still open in full generality. The problem asks:










