Related Research Articles
In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem with input size n is in NC if there exist constants c and k such that it can be solved in time O((log n)c) using O(nk) parallel processors. Stephen Cook coined the name "Nick's class" after Nick Pippenger, who had done extensive research on circuits with polylogarithmic depth and polynomial size.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.
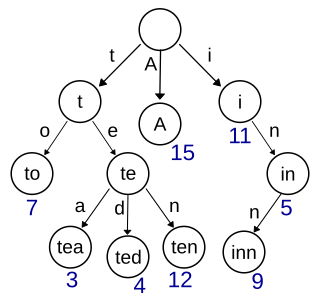
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In the theory of computation and automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton (NFA) into a deterministic finite automaton (DFA) which recognizes the same formal language. It is important in theory because it establishes that NFAs, despite their additional flexibility, are unable to recognize any language that cannot be recognized by some DFA. It is also important in practice for converting easier-to-construct NFAs into more efficiently executable DFAs. However, if the NFA has n states, the resulting DFA may have up to 2n states, an exponentially larger number, which sometimes makes the construction impractical for large NFAs.
In automata theory, a permutation automaton, or pure-group automaton, is a deterministic finite automaton such that each input symbol permutes the set of states.
In computer science, a linear bounded automaton is a restricted form of Turing machine.
In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.
In mathematics and theoretical computer science, an automatic sequence (also called a k-automatic sequence or a k-recognizable sequence when one wants to indicate that the base of the numerals used is k) is an infinite sequence of terms characterized by a finite automaton. The n-th term of an automatic sequence a(n) is a mapping of the final state reached in a finite automaton accepting the digits of the number n in some fixed base k.
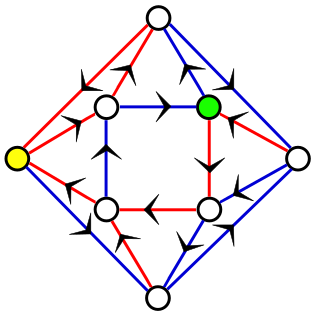
In computer science, more precisely, in the theory of deterministic finite automata (DFA), a synchronizing word or reset sequence is a word in the input alphabet of the DFA that sends any state of the DFA to one and the same state. That is, if an ensemble of copies of the DFA are each started in different states, and all of the copies process the synchronizing word, they will all end up in the same state. Not every DFA has a synchronizing word; for instance, a DFA with two states, one for words of even length and one for words of odd length, can never be synchronized.

In automata theory, DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum number of states. Here, two DFAs are called equivalent if they recognize the same regular language. Several different algorithms accomplishing this task are known and described in standard textbooks on automata theory.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
In automata theory, a branch of theoretical computer science, an ω-automaton is a variation of a finite automaton that runs on infinite, rather than finite, strings as input. Since ω-automata do not stop, they have a variety of acceptance conditions rather than simply a set of accepting states.
In computer science, the complexity function of a word or string is the function that counts the number of distinct factors of that string. More generally, the complexity function of a formal language counts the number of distinct words of given length.
In computational learning theory, induction of regular languages refers to the task of learning a formal description of a regular language from a given set of example strings. Although E. Mark Gold has shown that not every regular language can be learned this way, approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.
In automata theory, an unambiguous finite automaton (UFA) is a nondeterministic finite automaton (NFA) such that each word has at most one accepting path. Each deterministic finite automaton (DFA) is an UFA, but not vice versa. DFA, UFA, and NFA recognize exactly the same class of formal languages. On the one hand, an NFA can be exponentially smaller than an equivalent DFA. On the other hand, some problems are easily solved on DFAs and not on UFAs. For example, given an automaton A, an automaton A′ which accepts the complement of A can be computed in linear time when A is a DFA, whereas it is known that this cannot be done in polynomial time for UFAs. Hence UFAs are a mix of the worlds of DFA and of NFA; in some cases, they lead to smaller automata than DFA and quicker algorithms than NFA.
In mathematics, S2S is the monadic second order theory with two successors. It is one of the most expressive natural decidable theories known, with many decidable theories interpretable in S2S. Its decidability was proved by Rabin in 1969.
References
- 1 2 3 4 5 6 Demaine, Erik D.; Eisenstat, Sarah; Shallit, Jeffrey; Wilson, David A. (2011), "Remarks on separating words", Descriptional Complexity of Formal Systems: 13th International Workshop, DCFS 2011, Gießen/Limburg, Germany, July 25-27, 2011, Proceedings, Lecture Notes in Computer Science, vol. 6808, Heidelberg: Springer-Verlag, pp. 147–157, arXiv: 1103.4513 , doi:10.1007/978-3-642-22600-7_12, MR 2910373, S2CID 6959459 .
- ↑ Goralčík, P.; Koubek, V. (1986), "On discerning words by automata", Automata, Languages and Programming: 13th International Colloquium, Rennes, France, July 15–19, 1986, Proceedings, Lecture Notes in Computer Science, vol. 226, Berlin: Springer-Verlag, pp. 116–122, doi:10.1007/3-540-16761-7_61, MR 0864674 .
- ↑ Robson, J. M. (1989), "Separating strings with small automata", Information Processing Letters, 30 (4): 209–214, doi:10.1016/0020-0190(89)90215-9, MR 0986823 .
- ↑ Chase, Z. (2020), "A New Upper Bound for Separating Words", arXiv: 2007.12097 [math.CO].
- ↑ Chase, Zachary (2021-06-15). "Separating words and trace reconstruction". Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing. STOC 2021. New York, NY, USA: Association for Computing Machinery: 21–31. doi:10.1145/3406325.3451118. ISBN 978-1-4503-8053-9.
- ↑ Shallit, Jeffrey (2014), "Open Problems in Automata Theory: An Idiosyncratic View", British Colloquium for Theoretical Computer Science (BCTCS 2014), Loughborough University (PDF).