Shunt impedance

Last updated October 05, 2024

In accelerator physics, shunt impedance is a measure of the strength with which an eigenmode of a resonant radio frequency structure (e.g., in a microwave cavity) interacts with charged particles on a given straight line, typically along the axis of rotational symmetry. If not specified further, the term is likely to refer to longitudinal effective shunt impedance.

Longitudinal shunt impedance

To produce longitudinal Coulomb forces which add up to the (longitudinal) acceleration voltage $\scriptstyle V_{\parallel }$ , an eigenmode of the resonator has to be excited, leading to power dissipation $\scriptstyle P$ . The definition of the longitudinal effective shunt impedance, $\scriptstyle R$ , then reads:^[2]

R={\frac {|V_{\parallel }|^{2}}{P}}

with the longitudinal effective acceleration voltage $\scriptstyle |V_{\parallel }|$ .

The time-independent shunt impedance, $\scriptstyle R_{0}$ , with the time-independent acceleration voltage $\scriptstyle V_{0}$ is defined:^[2]

R_{0}={\frac {V_{0}^{2}}{P}}.

One can use the quality factor $\scriptstyle Q$ to substitute $\scriptstyle P$ with an equivalent expression:

R=Q{\frac {|V_{\parallel }|^{2}}{\omega W}},

where W is the maximum energy stored. Since the quality factor is the only quantity in the right equation term that depends on wall properties, the quantity $\scriptstyle {\frac {R}{Q}}$ is often used to design cavities, omitting material properties at first (see also cavity geometry factor).

Transverse shunt impedance

When a particle is deflected in transverse direction, the definition of the shunt impedance can be used with substitution of the (longitudinal) acceleration voltage by the transverse effective acceleration voltage, taking into account transversal Coulomb and Lorentz forces.

R_{\perp }={\frac {|V_{\perp }|^{2}}{P_{0}}}=Q{\frac {|V_{\perp }|^{2}}{\omega W}}

This does not necessarily imply a change in particle energy since a particle can also be deflected by magnetic fields (see Panofsky-Wenzel theorem).

Polarization angle

Because the transverse deflection can be described with polar coordinates, one may define a deflection or polarization angle using the transverse acceleration voltage components. Polar coordinates are used because it is possible to add up voltage components like vectors, but not shunt impedances.

Related Research Articles

A cyclotron is a type of particle accelerator invented by Ernest Lawrence in 1929–1930 at the University of California, Berkeley, and patented in 1932. A cyclotron accelerates charged particles outwards from the center of a flat cylindrical vacuum chamber along a spiral path. The particles are held to a spiral trajectory by a static magnetic field and accelerated by a rapidly varying electric field. Lawrence was awarded the 1939 Nobel Prize in Physics for this invention.

<span class="mw-page-title-main">Linear particle accelerator</span> Type of particle accelerator

A linear particle accelerator is a type of particle accelerator that accelerates charged subatomic particles or ions to a high speed by subjecting them to a series of oscillating electric potentials along a linear beamline. The principles for such machines were proposed by Gustav Ising in 1924, while the first machine that worked was constructed by Rolf Widerøe in 1928 at the RWTH Aachen University. Linacs have many applications: they generate X-rays and high energy electrons for medicinal purposes in radiation therapy, serve as particle injectors for higher-energy accelerators, and are used directly to achieve the highest kinetic energy for light particles for particle physics.

Accelerator physics is a branch of applied physics, concerned with designing, building and operating particle accelerators. As such, it can be described as the study of motion, manipulation and observation of relativistic charged particle beams and their interaction with accelerator structures by electromagnetic fields.

The multipactor effect is a phenomenon in radio-frequency (RF) amplifier vacuum tubes and waveguides, where, under certain conditions, secondary electron emission in resonance with an alternating electromagnetic field leads to exponential electron multiplication, possibly damaging and even destroying the RF device.

Quadrupole magnets, abbreviated as Q-magnets, consist of groups of four magnets laid out so that in the planar multipole expansion of the field, the dipole terms cancel and where the lowest significant terms in the field equations are quadrupole. Quadrupole magnets are useful as they create a magnetic field whose magnitude grows rapidly with the radial distance from its longitudinal axis. This is used in particle beam focusing.

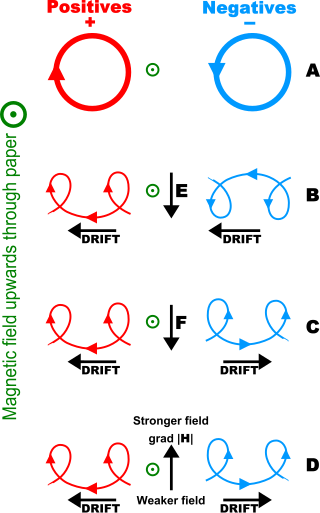
<span class="mw-page-title-main">Guiding center</span>

In physics, the motion of an electrically charged particle such as an electron or ion in a plasma in a magnetic field can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point. The drift speeds may differ for various species depending on their charge states, masses, or temperatures, possibly resulting in electric currents or chemical separation.

A Coulomb collision is a binary elastic collision between two charged particles interacting through their own electric field. As with any inverse-square law, the resulting trajectories of the colliding particles is a hyperbolic Keplerian orbit. This type of collision is common in plasmas where the typical kinetic energy of the particles is too large to produce a significant deviation from the initial trajectories of the colliding particles, and the cumulative effect of many collisions is considered instead. The importance of Coulomb collisions was first pointed out by Lev Landau in 1936, who also derived the corresponding kinetic equation which is known as the Landau kinetic equation.

In plasma physics, the Vlasov equation is a differential equation describing time evolution of the distribution function of collisionless plasma consisting of charged particles with long-range interaction, such as the Coulomb interaction. The equation was first suggested for the description of plasma by Anatoly Vlasov in 1938 and later discussed by him in detail in a monograph. The Vlasov equation, combined with Landau kinetic equation describe collisional plasma.

<span class="mw-page-title-main">Beam emittance</span> Property of a charged particle beam

In accelerator physics, emittance is a property of a charged particle beam. It refers to the area occupied by the beam in a position-and-momentum phase space.

Radiation damping in accelerator physics is a phenomenum where betatron oscillations and longitudinal oscilations of the particle are damped due to energy loss by synchrotron radiation. It can be used to reduce the beam emittance of a high-velocity charged particle beam.

Electron scattering occurs when electrons are displaced from their original trajectory. This is due to the electrostatic forces within matter interaction or, if an external magnetic field is present, the electron may be deflected by the Lorentz force. This scattering typically happens with solids such as metals, semiconductors and insulators; and is a limiting factor in integrated circuits and transistors.

Antenna measurement techniques refers to the testing of antennas in order to ensure that the antenna meets specifications or simply to characterize it. Typical antenna parameters are gain, bandwidth, radiation pattern, beamwidth, polarization, impedance; These are imperative communicative means.

A Wilson current mirror is a three-terminal circuit that accepts an input current at the input terminal and provides a "mirrored" current source or sink output at the output terminal. The mirrored current is a precise copy of the input current.

Zobel networks are a type of filter section based on the image-impedance design principle. They are named after Otto Zobel of Bell Labs, who published a much-referenced paper on image filters in 1923. The distinguishing feature of Zobel networks is that the input impedance is fixed in the design independently of the transfer function. This characteristic is achieved at the expense of a much higher component count compared to other types of filter sections. The impedance would normally be specified to be constant and purely resistive. For this reason, Zobel networks are also known as constant resistance networks. However, any impedance achievable with discrete components is possible.

<span class="mw-page-title-main">Superconducting radio frequency</span> Technique used to attain a high quality factor in resonant cavities

Superconducting radio frequency (SRF) science and technology involves the application of electrical superconductors to radio frequency devices. The ultra-low electrical resistivity of a superconducting material allows an RF resonator to obtain an extremely high quality factor, Q. For example, it is commonplace for a 1.3 GHz niobium SRF resonant cavity at 1.8 kelvins to obtain a quality factor of Q=5×10¹⁰. Such a very high Q resonator stores energy with very low loss and narrow bandwidth. These properties can be exploited for a variety of applications, including the construction of high-performance particle accelerator structures.

A microwave cavity or radio frequency cavity is a special type of resonator, consisting of a closed metal structure that confines electromagnetic fields in the microwave or RF region of the spectrum. The structure is either hollow or filled with dielectric material. The microwaves bounce back and forth between the walls of the cavity. At the cavity's resonant frequencies they reinforce to form standing waves in the cavity. Therefore, the cavity functions similarly to an organ pipe or sound box in a musical instrument, oscillating preferentially at a series of frequencies, its resonant frequencies. Thus it can act as a bandpass filter, allowing microwaves of a particular frequency to pass while blocking microwaves at nearby frequencies.

The primary line constants are parameters that describe the characteristics of conductive transmission lines, such as pairs of copper wires, in terms of the physical electrical properties of the line. The primary line constants are only relevant to transmission lines and are to be contrasted with the secondary line constants, which can be derived from them, and are more generally applicable. The secondary line constants can be used, for instance, to compare the characteristics of a waveguide to a copper line, whereas the primary constants have no meaning for a waveguide.

In accelerator physics, the term acceleration voltage means the effective voltage surpassed by a charged particle along a defined straight line. If not specified further, the term is likely to refer to the longitudinal effective acceleration voltage $.$

Impedance in Accelerator Physics is a quantity that characterizes the self interaction of a charged particle beam, mediated by the beam environment, such as the vacuum chamber, RF cavities, and other elements encountered along the accelerator or storage ring.

Accelerations in special relativity (SR) follow, as in Newtonian Mechanics, by differentiation of velocity with respect to time. Because of the Lorentz transformation and time dilation, the concepts of time and distance become more complex, which also leads to more complex definitions of "acceleration". SR as the theory of flat Minkowski spacetime remains valid in the presence of accelerations, because general relativity (GR) is only required when there is curvature of spacetime caused by the energy–momentum tensor. However, since the amount of spacetime curvature is not particularly high on Earth or its vicinity, SR remains valid for most practical purposes, such as experiments in particle accelerators.

References

↑ Lee, Shyh-Yuan (2004). Accelerator physics (2nd ed.). World Scientific. ISBN 978-981-256-200-5.
1 2 3 Wangler, Thomas (2008). RF Linear Accelerators (2nd ed.). Wiley-VCH. ISBN 978-3-527-62343-3. (slightly different notation)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[lee-1] Lee, Shyh-Yuan (2004). Accelerator physics (2nd ed.). World Scientific. ISBN 978-981-256-200-5.

[wangler-2] 1 2 3 Wangler, Thomas (2008). RF Linear Accelerators (2nd ed.). Wiley-VCH. ISBN 978-3-527-62343-3. (slightly different notation)

[1]

[2]