
Sim is a two-player paper-and-pencil game.

Sim is a two-player paper-and-pencil game.
Six dots (vertices) are drawn. Each dot is connected to every other dot by a line (edge).
Two players take turns coloring any uncolored lines. One player colors in one color, and the other colors in another color, with each player trying to avoid the creation of a triangle made solely of their color (only triangles with the dots as all corners count; intersections of lines are not relevant); the player who completes such a triangle loses immediately.
Ramsey theory can also be used to show that no game of Sim can end in a tie. Specifically, since the Ramsey number R(3, 3) is equal to 6, any two-coloring of the complete graph on 6 vertices (K6) must contain a monochromatic triangle, and therefore is not a tied position. This will also apply to any super-graph of K6. For another proof that there must eventually be a triangle of either color, see the Theorem on friends and strangers.
Computer search has verified that the second player can win Sim with perfect play, but finding a perfect strategy that humans can easily memorize is an open problem. [1]
The game of Sim is one example of a Ramsey game. Other Ramsey games are possible. For instance, the players can be allowed to color more than one line during their turns. Another Ramsey game similar to Sim and related to the Ramsey number R(4, 4) = 18 is played on 18 vertices and the 153 edges between them. The two players must avoid to color all six edges connecting four vertices.
Because the Ramsey number R(3, 3, 3) is equal to 17, any three-coloring of the complete graph on 17 vertices must contain a monochromatic triangle. A corresponding Ramsey game uses pencils of three colors. One approach can have three players compete, while another would allow two players to alternately select any of the three colors to paint an edge of the graph, until a player loses by completing a monochromatic triangle. Finding perfect winning strategies for these variants is most likely out of reach.
A technical report [2] by Wolfgang Slany is available online, with many references to literature on Sim, going back to the game's introduction by Gustavus Simmons in 1969, [3] including proofs and estimates of the difficulty as well as computational complexity of Sim and other Ramsey games.
A self-improving Java applet including its source code is available [4] for online play against a computer program.
An app including its source code in the visual multi-platform Catrobat programming language is available [5] for playing it against one's smartphone.
An electronic version is available at: https://wideaperture.net/sim/
In mathematics, the probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the result is of the prescribed kind is strictly greater than zero. Although the proof uses probability, the final conclusion is determined for certain, without any possible error.
In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
The Shannon switching game is a connection game for two players, invented by American mathematician and electrical engineer Claude Shannon, the "father of information theory" some time before 1951. Two players take turns coloring the edges of an arbitrary graph. One player has the goal of connecting two distinguished vertices by a path of edges of their color. The other player aims to prevent this by using their color instead. The game is commonly played on a rectangular grid; this special case of the game was independently invented by American mathematician David Gale in the late 1950s and is known as Gale or Bridg-It.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In mathematics, Sperner's lemma is a combinatorial result on colorings of triangulations, analogous to the Brouwer fixed point theorem, which is equivalent to it. It states that every Sperner coloring of a triangulation of an -dimensional simplex contains a cell whose vertices all have different colors.

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.

In graph theory and theoretical computer science, the monochromatic triangle problem is an algorithmic problem on graphs, in which the goal is to partition the edges of a given graph into two triangle-free subgraphs. It is NP-complete but fixed-parameter tractable on graphs of bounded treewidth.

The theorem on friends and strangers is a mathematical theorem in an area of mathematics called Ramsey theory.
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
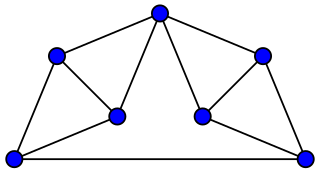
In graph theory, a branch of mathematics, the Moser spindle is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It is a unit distance graph requiring four colors in any graph coloring, and its existence can be used to prove that the chromatic number of the plane is at least four.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
In graph theory, a mixed graphG = (V, E, A) is a graph consisting of a set of vertices V, a set of (undirected) edges E, and a set of directed edges (or arcs) A.
The clique game is a positional game where two players alternately pick edges, trying to occupy a complete clique of a given size.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.