Related Research Articles

Positron emission tomography (PET) is a functional imaging technique that uses radioactive substances known as radiotracers to visualize and measure changes in metabolic processes, and in other physiological activities including blood flow, regional chemical composition, and absorption. Different tracers are used for various imaging purposes, depending on the target process within the body.
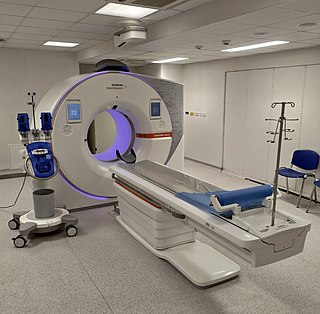
A computed tomography scan is a medical imaging technique used to obtain detailed internal images of the body. The personnel that perform CT scans are called radiographers or radiology technologists.

Avinash C. Kak is a professor of Electrical and Computer Engineering at Purdue University who has conducted pioneering research in several areas of information processing. His most noteworthy contributions deal with algorithms, languages, and systems related to networks, robotics, and computer vision. Born in Srinagar, Kashmir, he did his Bachelors in BE at University of Madras and Phd in Indian Institute of Technology Delhi. He joined the faculty of Purdue University in 1971.

Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, cosmochemistry, astrophysics, quantum information, and other areas of science. The word tomography is derived from Ancient Greek τόμος tomos, "slice, section" and γράφω graphō, "to write" or, in this context as well, "to describe." A device used in tomography is called a tomograph, while the image produced is a tomogram.

In digital image processing and computer vision, image segmentation is the process of partitioning a digital image into multiple image segments, also known as image regions or image objects. The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze. Image segmentation is typically used to locate objects and boundaries in images. More precisely, image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label share certain characteristics.

Electrical impedance tomography (EIT) is a noninvasive type of medical imaging in which the electrical conductivity, permittivity, and impedance of a part of the body is inferred from surface electrode measurements and used to form a tomographic image of that part. Electrical conductivity varies considerably among various biological tissues or the movement of fluids and gases within tissues. The majority of EIT systems apply small alternating currents at a single frequency, however, some EIT systems use multiple frequencies to better differentiate between normal and suspected abnormal tissue within the same organ.

Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.
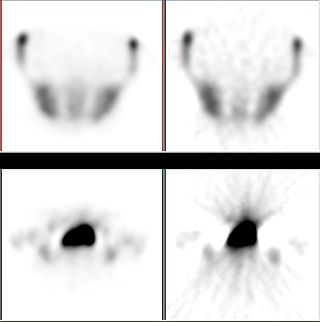
Iterative reconstruction refers to iterative algorithms used to reconstruct 2D and 3D images in certain imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step. In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization.

In radiography, X-ray microtomography uses X-rays to create cross-sections of a physical object that can be used to recreate a virtual model without destroying the original object. It is similar to tomography and X-ray computed tomography. The prefix micro- is used to indicate that the pixel sizes of the cross-sections are in the micrometre range. These pixel sizes have also resulted in creation of its synonyms high-resolution X-ray tomography, micro-computed tomography, and similar terms. Sometimes the terms high-resolution computed tomography (HRCT) and micro-CT are differentiated, but in other cases the term high-resolution micro-CT is used. Virtually all tomography today is computed tomography.

Discrete tomography focuses on the problem of reconstruction of binary images from a small number of their projections.
Mean shift is a non-parametric feature-space mathematical analysis technique for locating the maxima of a density function, a so-called mode-seeking algorithm. Application domains include cluster analysis in computer vision and image processing.
Compressed sensing is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Compressed sensing has applications in, for example, MRI where the incoherence condition is typically satisfied.
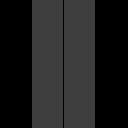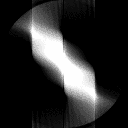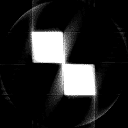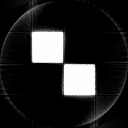
The algebraic reconstruction technique (ART) is an iterative reconstruction technique used in computed tomography. It reconstructs an image from a series of angular projections. Gordon, Bender and Herman first showed its use in image reconstruction; whereas the method is known as Kaczmarz method in numerical linear algebra.

Tomosynthesis, also digital tomosynthesis (DTS), is a method for performing high-resolution limited-angle tomography at radiation dose levels comparable with projectional radiography. It has been studied for a variety of clinical applications, including vascular imaging, dental imaging, orthopedic imaging, mammographic imaging, musculoskeletal imaging, and chest imaging.
Optical projection tomography is a form of tomography involving optical microscopy. The OPT technique is sometimes referred to as optical computed tomography (optical-CT) and optical emission computed tomography (optical-ECT) in the literature, to address the fact that the technique bears similarity to X-ray computed tomography (CT) and single-photon emission computed tomography (SPECT).
Coordinate descent is an optimization algorithm that successively minimizes along coordinate directions to find the minimum of a function. At each iteration, the algorithm determines a coordinate or coordinate block via a coordinate selection rule, then exactly or inexactly minimizes over the corresponding coordinate hyperplane while fixing all other coordinates or coordinate blocks. A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size. Coordinate descent is applicable in both differentiable and derivative-free contexts.

The computed tomography imaging spectrometer (CTIS) is a snapshot imaging spectrometer which can produce in fine the three-dimensional hyperspectral datacube of a scene.
Ultrasound computer tomography (USCT), sometimes also Ultrasound computed tomography, Ultrasound computerized tomography or just Ultrasound tomography, is a form of medical ultrasound tomography utilizing ultrasound waves as physical phenomenon for imaging. It is mostly in use for soft tissue medical imaging, especially breast imaging.
Four-dimensional computed tomography (4DCT) is a type of CT scanning which records multiple images over time. It allows playback of the scan as a video, so that physiological processes can be observed and internal movement can be tracked. The name is derived from the addition of time to traditional 3D computed tomography. Alternatively, the phase of a particular process, such as respiration, may be considered the fourth dimension.
Wojciech (Wojtek) Zbijewski is an American biomedical engineering and medical physics working in the fields of Computed tomography (CT), Cone beam computed tomography (CBCT), image reconstruction in CT, and applications of CT and CBCT in orthopedics. He is faculty at the Department of Biomedical Engineering at Johns Hopkins School of Medicine.
References
- ↑ Andersen, A.; Kak, A. (1984). "Simultaneous Algebraic Reconstruction Technique (SART): A Superior Implementation of ART". Ultrasonic Imaging. 6 (1): 81–94. doi:10.1016/0161-7346(84)90008-7. PMID 6548059.
- ↑ Pan, Jinxiao; Zhou, Tie; Han, Yan; Jiang, Ming (2006). "Variable Weighted Ordered Subset Image Reconstruction Algorithm". International Journal of Biomedical Imaging. 2006: 1–7. doi: 10.1155/IJBI/2006/10398 . PMC 2324020 . PMID 23165012.
- ↑ Zang, G.; Idoughi, R.; Tao, R.; Lubineau, G.; Wonka, P.; Heidrich, W. (2018). "Space-time Tomography for Continuously Deforming Objects". ACM Transactions on Graphics. 37 (4): 1–14. doi: 10.1145/3197517.3201298 . S2CID 5064003.
- ↑ Byrne, C. A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Problems 20 103 (2004)
- ↑ Jiang, M.; Wang, G. (2003). "Convergence of the simultaneous algebraic reconstruction technique (SART)". IEEE Transactions on Image Processing. 12 (8): 957–961. Bibcode:2003ITIP...12..957J. doi:10.1109/tip.2003.815295. PMID 18237969. S2CID 16267223.
- ↑ ftp://ftp.math.ucla.edu/pub/camreport/cam10-27.pdf
- ↑ "Abstract: EPS, Vol. 60 (No. 7), pp. 727-735".
- ↑ Batenburg, K.J.; Sijbers, J. (2011). "DART: a practical reconstruction algorithm for discrete tomography". IEEE Transactions on Image Processing. 20 (9): 2542–2553. Bibcode:2011ITIP...20.2542B. doi:10.1109/tip.2011.2131661. PMID 21435983. S2CID 16983053.