In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the relative order of equal elements is the same in the input and output. Merge sort is a divide-and-conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up merge sort appeared in a report by Goldstine and von Neumann as early as 1948.
Merge algorithms are a family of algorithms that take multiple sorted lists as input and produce a single list as output, containing all the elements of the inputs lists in sorted order. These algorithms are used as subroutines in various sorting algorithms, most famously merge sort.
In computer science, a red–black tree is a self-balancing binary search tree data structure noted for fast storage and retrieval of ordered information. The nodes in a red-black tree hold an extra "color" bit, often drawn as red and black, which help ensure that the tree is always approximately balanced.
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.
In computer science, selection sort is an in-place comparison sorting algorithm. It has a O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
In computer science, counting sort is an algorithm for sorting a collection of objects according to keys that are small positive integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that possess distinct key values, and applying prefix sum on those counts to determine the positions of each key value in the output sequence. Its running time is linear in the number of items and the difference between the maximum key value and the minimum key value, so it is only suitable for direct use in situations where the variation in keys is not significantly greater than the number of items. It is often used as a subroutine in radix sort, another sorting algorithm, which can handle larger keys more efficiently.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.

A join clause in the Structured Query Language (SQL) combines columns from one or more tables into a new table. The operation corresponds to a join operation in relational algebra. Informally, a join stitches two tables and puts on the same row records with matching fields : INNER, LEFT OUTER, RIGHT OUTER, FULL OUTER and CROSS.
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is also possible when the DAG has disconnected components.
In number theory, the integer square root (isqrt) of a non-negative integer n is the non-negative integer m which is the greatest integer less than or equal to the square root of n,
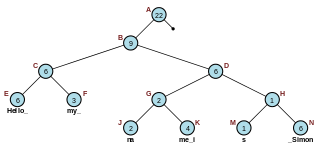
In computer programming, a rope, or cord, is a data structure composed of smaller strings that is used to efficiently store and manipulate longer strings or entire texts. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.
The hash join is an example of a join algorithm and is used in the implementation of a relational database management system. All variants of hash join algorithms involve building hash tables from the tuples of one or both of the joined relations, and subsequently probing those tables so that only tuples with the same hash code need to be compared for equality in equijoins.
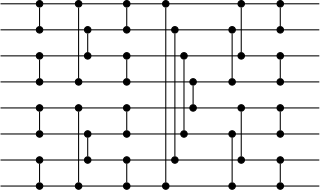
Bitonic mergesort is a parallel algorithm for sorting. It is also used as a construction method for building a sorting network. The algorithm was devised by Ken Batcher. The resulting sorting networks consist of comparators and have a delay of , where is the number of items to be sorted. This makes it a popular choice for sorting large numbers of elements on an architecture which itself contains a large number of parallel execution units running in lockstep, such as a typical GPU.

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
In computing, a procedural parameter is a parameter of a procedure that is itself a procedure.

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
Samplesort is a sorting algorithm that is a divide and conquer algorithm often used in parallel processing systems. Conventional divide and conquer sorting algorithms partitions the array into sub-intervals or buckets. The buckets are then sorted individually and then concatenated together. However, if the array is non-uniformly distributed, the performance of these sorting algorithms can be significantly throttled. Samplesort addresses this issue by selecting a sample of size s from the n-element sequence, and determining the range of the buckets by sorting the sample and choosing p−1 < s elements from the result. These elements then divide the array into p approximately equal-sized buckets. Samplesort is described in the 1970 paper, "Samplesort: A Sampling Approach to Minimal Storage Tree Sorting", by W. D. Frazer and A. C. McKellar.
In computer science, join-based tree algorithms are a class of algorithms for self-balancing binary search trees. This framework aims at designing highly-parallelized algorithms for various balanced binary search trees. The algorithmic framework is based on a single operation join. Under this framework, the join operation captures all balancing criteria of different balancing schemes, and all other functions join have generic implementation across different balancing schemes. The join-based algorithms can be applied to at least four balancing schemes: AVL trees, red–black trees, weight-balanced trees and treaps.