
Loop quantum gravity (LQG) is a theory of quantum gravity that incorporates matter of the Standard Model into the framework established for the intrinsic quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Albert Einstein's geometric formulation rather than the treatment of gravity as a mysterious mechanism (force). As a theory, LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale above the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.
In theoretical physics, twistor theory was proposed by Roger Penrose in 1967 as a possible path to quantum gravity and has evolved into a widely studied branch of theoretical and mathematical physics. Penrose's idea was that twistor space should be the basic arena for physics from which space-time itself should emerge. It has led to powerful mathematical tools that have applications to differential and integral geometry, nonlinear differential equations and representation theory, and in physics to general relativity, quantum field theory, and the theory of scattering amplitudes. Twistor theory arose in the context of the rapidly expanding mathematical developments in Einstein's theory of general relativity in the late 1950s and in the 1960s and carries a number of influences from that period. In particular, Roger Penrose has credited Ivor Robinson as an important early influence in the development of twistor theory, through his construction of so-called Robinson congruences.
Laurent Freidel is a French theoretical physicist and mathematical physicist known mainly for his contributions to quantum gravity, including loop quantum gravity, spin foam models, doubly special relativity, group field theory, relative locality and most recently metastring theory. He is currently a faculty member at Perimeter Institute for Theoretical Physics in Waterloo, Ontario, Canada.
Brane cosmology refers to several theories in particle physics and cosmology related to string theory, superstring theory and M-theory.
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity (LQG), a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units. As a result, its value is currently fixed by matching the semiclassical black hole entropy, as calculated by Stephen Hawking, and the counting of microstates in loop quantum gravity.
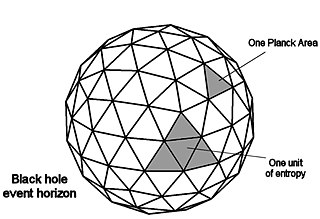
In physics, the Bekenstein bound is an upper limit on the thermodynamic entropy S, or Shannon entropy H, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximal amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy are finite. In computer science this implies that non-finite models such as Turing machines are not realizable as finite devices.
Tamiaki Yoneya is a Japanese physicist.

Helen Fay Dowker is a British physicist who is a current professor of theoretical physics at Imperial College London.
In theoretical particle physics, the non-commutative Standard Model, is a model based on noncommutative geometry that unifies a modified form of general relativity with the Standard Model.
In physical cosmology, fractal cosmology is a set of minority cosmological theories which state that the distribution of matter in the Universe, or the structure of the universe itself, is a fractal across a wide range of scales. More generally, it relates to the usage or appearance of fractals in the study of the universe and matter. A central issue in this field is the fractal dimension of the universe or of matter distribution within it, when measured at very large or very small scales.
In particle physics and string theory (M-theory), the ADD model, also known as the model with large extra dimensions (LED), is a model framework that attempts to solve the hierarchy problem. The model tries to explain this problem by postulating that our universe, with its four dimensions, exists on a membrane in a higher dimensional space. It is then suggested that the other forces of nature operate within this membrane and its four dimensions, while the hypothetical gravity-bearing particle, the graviton, can propagate across the extra dimensions. This would explain why gravity is very weak compared to the other fundamental forces. The size of the dimensions in ADD is around the order of the TeV scale, which results in it being experimentally probeable by current colliders, unlike many exotic extra dimensional hypotheses that have the relevant size around the Planck scale.
In mathematical physics, de Sitter invariant special relativity is the speculative idea that the fundamental symmetry group of spacetime is the indefinite orthogonal group SO(4,1), that of de Sitter space. In the standard theory of general relativity, de Sitter space is a highly symmetrical special vacuum solution, which requires a cosmological constant or the stress–energy of a constant scalar field to sustain.
In mathematical physics, the concept of quantum spacetime is a generalization of the usual concept of spacetime in which some variables that ordinarily commute are assumed not to commute and form a different Lie algebra. The choice of that algebra still varies from theory to theory. As a result of this change some variables that are usually continuous may become discrete. Often only such discrete variables are called "quantized"; usage varies.

Group field theory (GFT) is a quantum field theory in which the base manifold is taken to be a Lie group. It is closely related to background independent quantum gravity approaches such as loop quantum gravity, the spin foam formalism and causal dynamical triangulation. It can be shown that its perturbative expansion can be interpreted as spin foams and simplicial pseudo-manifolds (depending on the representation of the fields). Thus, its partition function defines a non-perturbative sum over all simplicial topologies and geometries, giving a path integral formulation of quantum spacetime.

In strong interaction physics, light front holography or light front holographic QCD is an approximate version of the theory of quantum chromodynamics (QCD) which results from mapping the gauge theory of QCD to a higher-dimensional anti-de Sitter space (AdS) inspired by the AdS/CFT correspondence proposed for string theory. This procedure makes it possible to find analytic solutions in situations where strong coupling occurs, improving predictions of the masses of hadrons and their internal structure revealed by high-energy accelerator experiments. The most widely used approach to finding approximate solutions to the QCD equations, lattice QCD, has had many successful applications; however, it is a numerical approach formulated in Euclidean space rather than physical Minkowski space-time.

Asymptotic safety is a concept in quantum field theory which aims at finding a consistent and predictive quantum theory of the gravitational field. Its key ingredient is a nontrivial fixed point of the theory's renormalization group flow which controls the behavior of the coupling constants in the ultraviolet (UV) regime and renders physical quantities safe from divergences. Although originally proposed by Steven Weinberg to find a theory of quantum gravity, the idea of a nontrivial fixed point providing a possible UV completion can be applied also to other field theories, in particular to perturbatively nonrenormalizable ones. In this respect, it is similar to quantum triviality.
Dynamical dimensional reduction or spontaneous dimensional reduction is the apparent reduction in the number of spacetime dimensions as a function of the distance scale, or conversely the energy scale, with which spacetime is probed. At least within the current level of experimental precision, our universe has three dimensions of space and one of time. However, the idea that the number of dimensions may increase at extremely small length scales was first proposed more than a century ago, and is now fairly commonplace in theoretical physics. Contrary to this, a number of recent results in quantum gravity suggest the opposite behavior, a dynamical reduction of the number of spacetime dimensions at small length scales.
A. W. Peet is a professor of physics at the University of Toronto. Peet's research interests include string theory as a quantum theory of gravity, quantum field theory and applications of string theory to black holes, gauge theories, cosmology, and the correspondence between anti-de Sitter space and conformal field theories.
Higher-spin theory or higher-spin gravity is a common name for field theories that contain massless fields of spin greater than two. Usually, the spectrum of such theories contains the graviton as a massless spin-two field, which explains the second name. Massless fields are gauge fields and the theories should be (almost) completely fixed by these higher-spin symmetries. Higher-spin theories are supposed to be consistent quantum theories and, for this reason, to give examples of quantum gravity. Most of the interest in the topic is due to the AdS/CFT correspondence where there is a number of conjectures relating higher-spin theories to weakly coupled conformal field theories. It is important to note that only certain parts of these theories are known at present and not many examples have been worked out in detail except some specific toy models.
Hermann Nicolai is a German theoretical physicist and director emeritus at the Max Planck Institute for Gravitational Physics in Potsdam-Golm.








