Related Research Articles
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
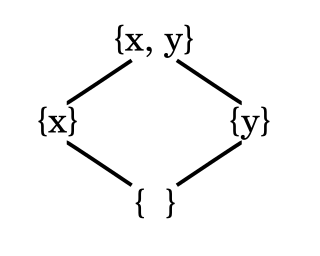
In order theory, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set one represents each element of as a vertex in the plane and draws a line segment or curve that goes upward from one vertex to another vertex whenever covers . These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two distinct elements in the subset are incomparable.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.
In combinatorics, a Sperner family, or clutter, is a family F of subsets of a finite set E in which none of the sets contains another. Equivalently, a Sperner family is an antichain in the inclusion lattice over the power set of E. A Sperner family is also sometimes called an independent system or irredundant set.
Sperner's theorem, in discrete mathematics, describes the largest possible families of finite sets none of which contain any other sets in the family. It is one of the central results in extremal set theory. It is named after Emanuel Sperner, who published it in 1928.
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).
In mathematics, specifically order theory, a partially ordered set is chain-complete if every chain in it has a least upper bound. It is ω-complete when every increasing sequence of elements has a least upper bound; the same notion can be extended to other cardinalities of chains.

In mathematics, in the branch of combinatorics, a graded poset is a partially-ordered set (poset) P equipped with a rank functionρ from P to the set N of all natural numbers. ρ must satisfy the following two properties:
G. W. Peck is a pseudonymous attribution used as the author or co-author of a number of published mathematics academic papers. Peck is sometimes humorously identified with George Wilbur Peck, a former governor of the US state of Wisconsin.

In mathematics, Young's lattice is a lattice that is formed by all integer partitions. It is named after Alfred Young, who, in a series of papers On quantitative substitutional analysis, developed the representation theory of the symmetric group. In Young's theory, the objects now called Young diagrams and the partial order on them played a key, even decisive, role. Young's lattice prominently figures in algebraic combinatorics, forming the simplest example of a differential poset in the sense of Stanley (1988). It is also closely connected with the crystal bases for affine Lie algebras.
In mathematics, specifically order theory, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains it. It is named after Holbrook Mann MacNeille whose 1937 paper first defined and constructed it, and after Richard Dedekind because its construction generalizes the Dedekind cuts used by Dedekind to construct the real numbers from the rational numbers. It is also called the completion by cuts or normal completion.

In mathematics, the Dedekind numbers are a rapidly growing sequence of integers named after Richard Dedekind, who defined them in 1897. The Dedekind number M(n) counts the number of monotone boolean functions of n variables. Equivalently, it counts the number of antichains of subsets of an n-element set, the number of elements in a free distributive lattice with n generators, or the number of abstract simplicial complexes with n elements.

In mathematics, a fence, also called a zigzag poset, is a partially ordered set (poset) in which the order relations form a path with alternating orientations:
In order theory, a branch of mathematics, the 1/3–2/3 conjecture states that, if one is comparison sorting a set of items then, no matter what comparisons may have already been performed, it is always possible to choose the next comparison in such a way that it will reduce the number of possible sorted orders by a factor of 2/3 or better. Equivalently, in every finite partially ordered set that is not totally ordered, there exists a pair of elements x and y with the property that at least 1/3 and at most 2/3 of the linear extensions of the partial order place x earlier than y.
In mathematics, in the areas of order theory and combinatorics, Mirsky's theorem characterizes the height of any finite partially ordered set in terms of a partition of the order into a minimum number of antichains. It is named for Leon Mirsky (1971) and is closely related to Dilworth's theorem on the widths of partial orders, to the perfection of comparability graphs, to the Gallai–Hasse–Roy–Vitaver theorem relating longest paths and colorings in graphs, and to the Erdős–Szekeres theorem on monotonic subsequences.
In mathematics, a differential poset is a partially ordered set satisfying certain local properties. This family of posets was introduced by Stanley (1988) as a generalization of Young's lattice, many of whose combinatorial properties are shared by all differential posets. In addition to Young's lattice, the other most significant example of a differential poset is the Young–Fibonacci lattice.
In mathematics, the order polytope of a finite partially ordered set is a convex polytope defined from the set. The points of the order polytope are the monotonic functions from the given set to the unit interval, its vertices correspond to the upper sets of the partial order, and its dimension is the number of elements in the partial order. The order polytope is a distributive polytope, meaning that coordinatewise minima and maxima of pairs of its points remain within the polytope.
References
- 1 2 Stanley, Richard (1984), "Quotients of Peck posets", Order, 1 (1): 29–34, doi:10.1007/BF00396271, MR 0745587, S2CID 14857863 .
- 1 2 3 4 Handbook of discrete and combinatorial mathematics, by Kenneth H. Rosen, John G. Michaels
- ↑ Graham, R. L. (June 1978), "Maximum antichains in the partition lattice" (PDF), The Mathematical Intelligencer , 1 (2): 84–86, doi:10.1007/BF03023067, MR 0505555, S2CID 120190991