
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order."
In mathematics, a total or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation on some set , which satisfies the following for all and in :
- (reflexive).
- If and then (transitive).
- If and then (antisymmetric).
- or .
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.

In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included. Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.
In combinatorics, a Sperner family, or clutter, is a family F of subsets of a finite set E in which none of the sets contains another. Equivalently, a Sperner family is an antichain in the inclusion lattice over the power set of E. A Sperner family is also sometimes called an independent system or irredundant set.
Sperner's theorem, in discrete mathematics, describes the largest possible families of finite sets none of which contain any other sets in the family. It is one of the central results in extremal set theory. It is named after Emanuel Sperner, who published it in 1928.
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).
In mathematics, a join-semilattice is a partially ordered set that has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset. Every join-semilattice is a meet-semilattice in the inverse order and vice versa.
In mathematics, a Riesz space, lattice-ordered vector space or vector lattice is a partially ordered vector space where the order structure is a lattice.

In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours. The covering relation is commonly used to graphically express the partial order by means of the Hasse diagram.
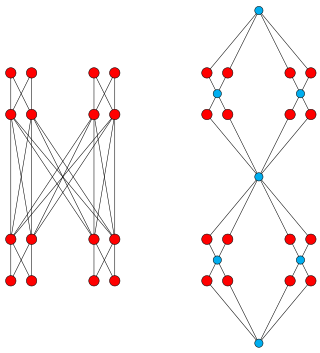
In mathematics, specifically order theory, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains it. It is named after Holbrook Mann MacNeille whose 1937 paper first defined and constructed it, and after Richard Dedekind because its construction generalizes the Dedekind cuts used by Dedekind to construct the real numbers from the rational numbers. It is also called the completion by cuts or normal completion.
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets. The theorem can be interpreted as providing a one-to-one correspondence between distributive lattices and partial orders, between quasi-ordinal knowledge spaces and preorders, or between finite topological spaces and preorders. It is named after Garrett Birkhoff, who published a proof of it in 1937.

In mathematics, the Dedekind numbers are a rapidly growing sequence of integers named after Richard Dedekind, who defined them in 1897. The Dedekind number M(n) counts the number of monotone boolean functions of n variables. Equivalently, it counts the number of antichains of subsets of an n-element set, the number of elements in a free distributive lattice with n generators, or the number of abstract simplicial complexes with n elements.
In mathematics, in the areas of order theory and combinatorics, Mirsky's theorem characterizes the height of any finite partially ordered set in terms of a partition of the order into a minimum number of antichains. It is named for Leon Mirsky (1971) and is closely related to Dilworth's theorem on the widths of partial orders, to the perfection of comparability graphs, to the Gallai–Hasse–Roy–Vitaver theorem relating longest paths and colorings in graphs, and to the Erdős–Szekeres theorem on monotonic subsequences.
In mathematics, the order polytope of a finite partially ordered set is a convex polytope defined from the set. The points of the order polytope are the monotonic functions from the given set to the unit interval, its vertices correspond to the upper sets of the partial order, and its dimension is the number of elements in the partial order. The order polytope is a distributive polytope, meaning that coordinatewise minima and maxima of pairs of its points remain within the polytope.
In mathematics, economics, and computer science, the lattice of stable matchings is a distributive lattice whose elements are stable matchings. For a given instance of the stable matching problem, this lattice provides an algebraic description of the family of all solutions to the problem. It was originally described in the 1970s by John Horton Conway and Donald Knuth.






















