In combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory, design of robust computer networks, and the theory of error-correcting codes.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking.
In combinatorial mathematics, Ramsey's theorem states that one will find monochromatic cliques in any edge labelling of a sufficiently large complete graph. To demonstrate the theorem for two colours, let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices.

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. Formally, a hypergraph is a pair where is a set of elements called nodes or vertices, and is a set of non-empty subsets of called hyperedges or edges. Therefore, is a subset of , where is the power set of .

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.

In the mathematical discipline of graph theory, a vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set. The problem of finding a minimum vertex cover is a classical optimization problem in computer science and is a typical example of an NP-hard optimization problem that has an approximation algorithm. Its decision version, the vertex cover problem, was one of Karp's 21 NP-complete problems and is therefore a classical NP-complete problem in computational complexity theory. Furthermore, the vertex cover problem is fixed-parameter tractable and a central problem in parameterized complexity theory.
In the mathematical discipline of graph theory, a matching or independent edge set in a graph is a set of edges without common vertices. Finding a matching in a bipartite graph can be treated as a network flow problem.
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth (1950).
In mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. Szemerédi (1975) introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove Szemerédi's theorem, and in he proved the full lemma. Extensions of the regularity method to hypergraphs were obtained by Rödl and his collaborators and Gowers.
In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

A vertex model is a type of statistical mechanics model in which the Boltzmann weights are associated with a vertex in the model. This contrasts with a nearest-neighbour model, such as the Ising model, in which the energy, and thus the Boltzmann weight of a statistical microstate is attributed to the bonds connecting two neighbouring particles. The energy associated with a vertex in the lattice of particles is thus dependent on the state of the bonds which connect it to adjacent vertices. It turns out that every solution of the Yang-Baxter equation with spectral parameters in a tensor product of vector spaces yields an exactly-solvable vertex model.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
In the mathematical discipline of graph theory, the Erdős–Pósa theorem, named after Paul Erdős and Lajos Pósa, states that there is a function f(k) such that for each positive integer k, every graph either contains k vertex-disjoint circuits or it has a feedback vertex set of f(k) vertices that intersects every circuit. Furthermore, f(k) = O(k log k) in the sense of Big O notation. Because of this theorem, circuits are said to have the Erdős–Pósa property.
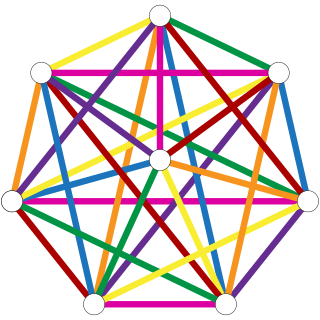
In combinatorial mathematics, Baranyai's theorem deals with the decompositions of complete hypergraphs.
In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.
In geometry, specifically projective geometry, a blocking set is a set of points in a projective plane which every line intersects and which does not contain an entire line. The concept can be generalized in several ways. Instead of talking about points and lines, one could deal with n-dimensional subspaces and m-dimensional subspaces, or even more generally, objects of type 1 and objects of type 2 when some concept of intersection makes sense for these objects. A second way to generalize would be to move into more abstract settings than projective geometry. One can define a blocking set of a hypergraph as a set that meets all edges of the hypergraph.































