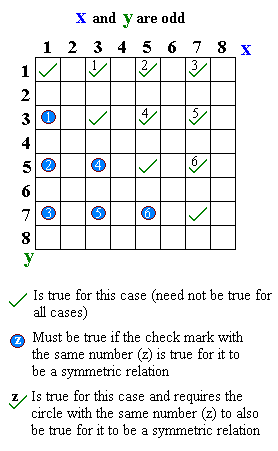
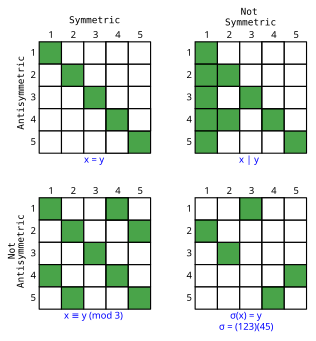
In mathematics, a binary relation on a set is antisymmetric if there is no pair of distinct elements of each of which is related by to the other. More formally, is antisymmetric precisely if for all
In mathematics, a binary relation associates elements of one set, called the domain, with elements of another set, called the codomain. A binary relation over sets and is a set of ordered pairs consisting of elements from and from . It is a generalization of the more widely understood idea of a unary function. It encodes the common concept of relation: an element is related to an element , if and only if the pair belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case of an -ary relation over sets , which is a subset of the Cartesian product

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equality. Any number is equal to itself (reflexive). If , then (symmetric). If and , then (transitive).

In mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive and transitive. The name preorder is meant to suggest that preorders are almost partial orders, but not quite, as they are not necessarily antisymmetric.
In mathematics, equality is a relationship between two quantities or, more generally, two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. Equality between A and B is written A = B, and pronounced "A equals B". The symbol "=" is called an "equals sign". Two objects that are not equal are said to be distinct.
In mathematics, a binary relation on a set is reflexive if it relates every element of to itself.
In mathematics, a binary relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates a to c.
In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: 1 − 2 is not a natural number, although both 1 and 2 are.

Asymmetry is the absence of, or a violation of, symmetry. Symmetry is an important property of both physical and abstract systems and it may be displayed in precise terms or in more aesthetic terms. The absence of or violation of symmetry that are either expected or desired can have important consequences for a system.
In mathematics, an asymmetric relation is a binary relation on a set where for all if is related to then is not related to
In mathematics, a partial equivalence relation is a homogeneous binary relation that is symmetric and transitive. If the relation is also reflexive, then the relation is an equivalence relation.
This article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC and in NFU, the version of Quine's New Foundations shown to be consistent by R. B. Jensen in 1969.

In mathematics, two elements x and y of a set P are said to be comparable with respect to a binary relation ≤ if at least one of x ≤ y or y ≤ x is true. They are called incomparable if they are not comparable.

The mathematical notion of quasitransitivity is a weakened version of transitivity that is used in social choice theory and microeconomics. Informally, a relation is quasitransitive if it is symmetric for some values and transitive elsewhere. The concept was introduced by Sen (1969) to study the consequences of Arrow's theorem.
In mathematics, Euclidean relations are a class of binary relations that formalize "Axiom 1" in Euclid's Elements: "Magnitudes which are equal to the same are equal to each other."
In mathematics, a homogeneous relation on a set X is a binary relation between X and itself, i.e. it is a subset of the Cartesian product X × X. This is commonly phrased as "a relation on X" or "a (binary) relation over X". An example of a homogeneous relation is the relation of kinship, where the relation is between people.
In mathematical logic, the ancestral relation of a binary relation R is its transitive closure, however defined in a different way, see below.

In mathematics, a relation on a set may, or may not, hold between two given members of the set. As an example, "is less than" is a relation on the set of natural numbers; it holds, for instance, between the values 1 and 3, and likewise between 3 and 4, but not between the values 3 and 1 nor between 4 and 4, that is, 3 < 1 and 4 < 4 both evaluate to false. As another example, "is sister of" is a relation on the set of all people, it holds e.g. between Marie Curie and Bronisława Dłuska, and likewise vice versa. Set members may not be in relation "to a certain degree" – either they are in relation or they are not.
In order theory, the Szpilrajn extension theorem, proved by Edward Szpilrajn in 1930, states that every partial order is contained in a total order. Intuitively, the theorem says that any method of comparing elements that leaves some pairs incomparable can be extended in such a way that every pair becomes comparable. The theorem is one of many examples of the use of the axiom of choice in the form of Zorn's lemma to find a maximal set with certain properties.
In mathematics, an idempotent binary relation is a binary relation R on a set X for which the composition of relations R ∘ R is the same as R. This notion generalizes that of an idempotent function to relations.