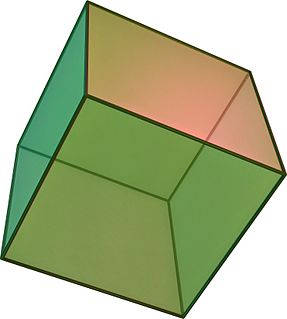
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface such as a plane or the surface of a cylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional because three coordinates are needed to locate a point within these spaces.
In mathematics, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space. The conjecture states:
Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.
24 (twenty-four) is the natural number following 23 and preceding 25.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, n-dimensional Euclidean space or to non-Euclidean spaces such as hyperbolic space.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
In geometry, a kissing number is defined as the number of non-overlapping unit spheres that can be arranged such that they each touch a common unit sphere. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another. Other names for kissing number that have been used are Newton number, and contact number.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space. A clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.

A four-dimensional space or 4D space is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible generalization of the observation that one only needs three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring its length, width, and height.
In the mathematical area of topology, the Generalized Poincaré conjecture is a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a category of manifolds: topological (Top), piecewise linear (PL), or differentiable (Diff). Then the statement is

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.

In four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular space-filling tessellation of 4-dimensional Euclidean space by regular 24-cells. It can be represented by Schläfli symbol {3,4,3,3}.
The 5-demicube honeycomb, or demipenteractic honeycomb is a uniform space-filling tessellation in Euclidean 5-space. It is constructed as an alternation of the regular 5-cube honeycomb.
The 8-demicubic honeycomb, or demiocteractic honeycomb is a uniform space-filling tessellation in Euclidean 8-space. It is constructed as an alternation of the regular 8-cubic honeycomb.

In geometry of higher dimensions, a hypersphere is the set of points at a constant distance from a given point called its centre. It is a manifold of codimension one—that is, with one dimension less than that of the ambient space.
Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.
In mathematics, a sequence of n real numbers can be understood as a location in n-dimensional space. When n = 7, the set of all such locations is called 7-dimensional space. Often such a space is studied as a vector space, without any notion of distance. Seven-dimensional Euclidean space is seven-dimensional space equipped with a Euclidean metric, which is defined by the dot product.
In mathematics, a sequence of n real numbers can be understood as a location in n-dimensional space. When n = 8, the set of all such locations is called 8-dimensional space. Often such spaces are studied as vector spaces, without any notion of distance. Eight-dimensional Euclidean space is eight-dimensional space equipped with the Euclidean metric.

In geometry, the simplectic honeycomb is a dimensional infinite series of honeycombs, based on the affine Coxeter group symmetry. It is given a Schläfli symbol {3[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. It can be thought of as an n-dimensional hypercubic honeycomb that has been subdivided along all hyperplanes , then stretched along its main diagonal until the simplices on the ends of the hypercubes become regular. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.












