Related Research Articles
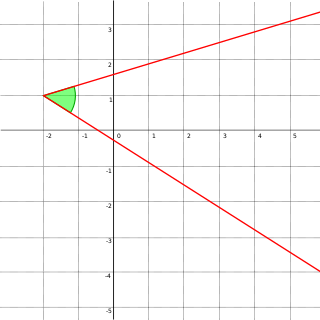
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system the base unit for length is the metre.

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

In mathematics, an n-sphere or hypersphere is an n-dimensional generalization of the 1-dimensional circle and 2-dimensional sphere to any non-negative integer n. The n-sphere is the setting for n-dimensional spherical geometry.
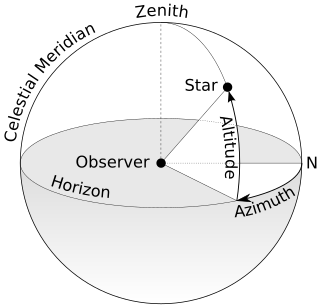
An azimuth is the angular measurement in a spherical coordinate system which represents the horizontal angle from a cardinal direction, most commonly north.

In astronomy and celestial navigation, the hour angle is the dihedral angle between the meridian plane and the hour circle.

In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the x-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and vice versa; this is the basis of analytic geometry.

In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,

Spherical geometry or spherics is the geometry of the two-dimensional surface of a sphere or the n-dimensional surface of higher dimensional spheres.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
The angular diameter, angular size, apparent diameter, or apparent size is an angular distance describing how large a sphere or circle appears from a given point of view. In the vision sciences, it is called the visual angle, and in optics, it is the angular aperture. The angular diameter can alternatively be thought of as the angular displacement through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side. Humans can resolve with their naked eyes diameters down to about 1 arcminute. This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus as a disk under optimal conditions.

A coordinate-measuring machine (CMM) is a device that measures the geometry of physical objects by sensing discrete points on the surface of the object with a probe. Various types of probes are used in CMMs, the most common being mechanical and laser sensors, though optical and white light sensors do exist. Depending on the machine, the probe position may be manually controlled by an operator, or it may be computer controlled. CMMs typically specify a probe's position in terms of its displacement from a reference position in a three-dimensional Cartesian coordinate system. In addition to moving the probe along the X, Y, and Z axes, many machines also allow the probe angle to be controlled to allow measurement of surfaces that would otherwise be unreachable.
Roundness is the measure of how closely the shape of an object approaches that of a mathematically perfect circle. Roundness applies in two dimensions, such as the cross sectional circles along a cylindrical object such as a shaft or a cylindrical roller for a bearing. In geometric dimensioning and tolerancing, control of a cylinder can also include its fidelity to the longitudinal axis, yielding cylindricity. The analogue of roundness in three dimensions is sphericity.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.
The mathematics of general relativity is complex. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function, cosine function, and versine function.
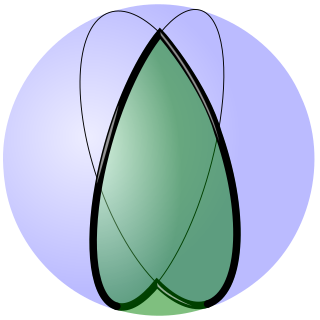
In spherical geometry, a spherical lune is an area on a sphere bounded by two half great circles which meet at antipodal points. It is an example of a digon, {2}θ, with dihedral angle θ. The word "lune" derives from luna, the Latin word for Moon.

In four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball of radius r1 and a line segment of length 2r2:
References
- ↑ Green, Robin Michael (1985). Spherical Astronomy. Cambridge University Press. p. 3. ISBN 9780521317795.
- ↑ Atatürk, Mustafa Kemal (1936). Geometri. İş Bankası Kültür Yayınları. ISBN 9786254050428.[ page needed ]