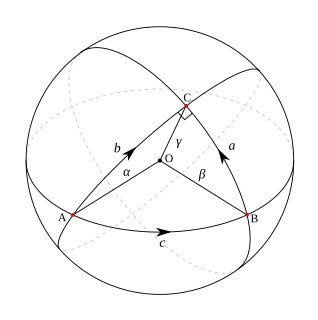
In differential geometry, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor is the most common method used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold, that measures the extent to which the metric tensor is not locally isometric to that of Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection.

In differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in M. As a set, it is given by the disjoint union of the tangent spaces of M. That is,
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a unified approach to define integrands over curves, surfaces, volumes, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics.
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport must be linear. Such a connection is equivalently specified by a covariant derivative, which is an operator that can differentiate sections of that bundle along tangent directions in the base manifold. Connections in this sense generalize, to arbitrary vector bundles, the concept of a linear connection on the tangent bundle of a smooth manifold, and are sometimes known as linear connections. Nonlinear connections are connections that are not necessarily linear in this sense.
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, i.e., a smooth manifold whose points are probability measures defined on a common probability space. It can be used to calculate the informational difference between measurements.
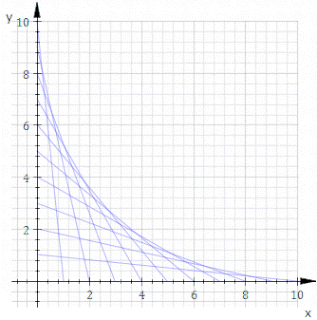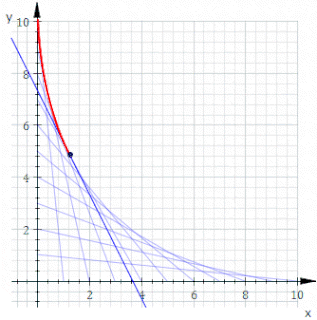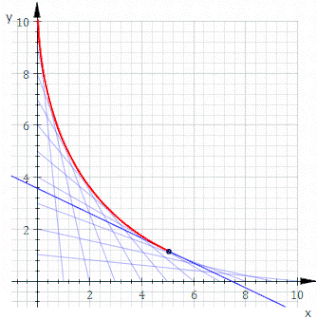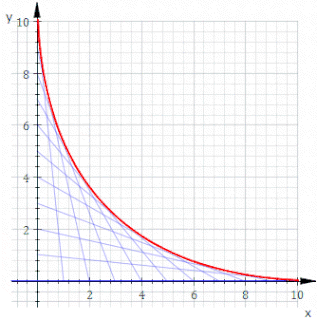
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.
In differential topology, the jet bundle is a certain construction that makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form. Jets may also be seen as the coordinate free versions of Taylor expansions.

The mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
In general relativity, geodesic deviation describes the tendency of objects to approach or recede from one another while moving under the influence of a spatially varying gravitational field. Put another way, if two objects are set in motion along two initially parallel trajectories, the presence of a tidal gravitational force will cause the trajectories to bend towards or away from each other, producing a relative acceleration between the objects.
In differential geometry, a Lie algebra-valued form is a differential form with values in a Lie algebra. Such forms have important applications in the theory of connections on a principal bundle as well as in the theory of Cartan connections.
In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the plane of curvature. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas.
In mathematics, the vertical bundle and the horizontal bundle are two subbundles of the tangent bundle of a smooth fiber bundle, forming complementary subspaces at each point of the fibre bundle. The vertical bundle consists of all vectors that are tangent to the fibers, while the horizontal bundle is then a particular choice of a subbundle of the tangent bundle which is complementary to the vertical bundle.
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G. The key examples are the matrix coefficients of the spherical principal series, the irreducible representations appearing in the decomposition of the unitary representation of G on L2(G/K). In this case the commutant of G is generated by the algebra of biinvariant functions on G with respect to K acting by right convolution. It is commutative if in addition G/K is a symmetric space, for example when G is a connected semisimple Lie group with finite centre and K is a maximal compact subgroup. The matrix coefficients of the spherical principal series describe precisely the spectrum of the corresponding C* algebra generated by the biinvariant functions of compact support, often called a Hecke algebra. The spectrum of the commutative Banach *-algebra of biinvariant L1 functions is larger; when G is a semisimple Lie group with maximal compact subgroup K, additional characters come from matrix coefficients of the complementary series, obtained by analytic continuation of the spherical principal series.
In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form. These concepts were put in their current form with principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.
Photon sphere (definition):
A photon sphere of a static spherically symmetric metric is a timelike hypersurface if the deflection angle of a light ray with the closest distance of approach diverges as












