Related Research Articles

The wave equation is an important second-order linear partial differential equation for the description of waves—as they occur in classical physics—such as mechanical waves or light waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as

In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
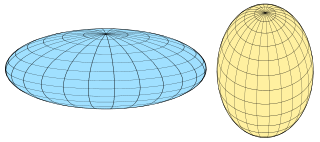
A spheroid, or ellipsoid of revolution, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.
In classical mechanics, the gravitational potential at a location is equal to the work per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation:
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space. This problem isn't exactly solvable, and yields an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange, Liouville, Laplace, Jacobi, Darboux, Le Verrier, Velde, Hamilton, Poincaré, Birkhoff and E. T. Whittaker, among others.

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
In mathematics, the spheroidal wave equation is given by
In quantum mechanics, the spinor spherical harmonics are special functions defined over the sphere. The spinor spherical harmonics are the natural spinor analog of the vector spherical harmonics. While the standard spherical harmonics are a basis for the angular momentum operator, the spinor spherical harmonics are a basis for the total angular momentum operator. These functions are used in analytical solutions to Dirac equation in a radial potential. The spinor spherical harmonics are sometimes called Pauli central field spinors, in honor to Wolfgang Pauli who employed them in the solution of the hydrogen atom with spin–orbit interaction.
In physics, the Green's function for Laplace's equation in three variables is used to describe the response of a particular type of physical system to a point source. In particular, this Green's function arises in systems that can be described by Poisson's equation, a partial differential equation (PDE) of the form
In mathematics, the Prolate spheroidal wave functions (PSWF) are a set of orthogonal bandlimited functions. They are eigenfunctions of a timelimiting operation followed by a lowpassing operation. Let denote the time truncation operator, such that if and only if is timelimited within . Similarly, let denote an ideal low-pass filtering operator, such that if and only if is bandlimited within . The operator turns out to be linear, bounded and self-adjoint. For we denote with the n-th eigenfunction, defined as
In mathematics, a Lamé function, or ellipsoidal harmonic function, is a solution of Lamé's equation, a second-order ordinary differential equation. It was introduced in the paper. Lamé's equation appears in the method of separation of variables applied to the Laplace equation in elliptic coordinates. In some special cases solutions can be expressed in terms of polynomials called Lamé polynomials.

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.
In applied mathematics, oblate spheroidal wave functions are involved in the solution of the Helmholtz equation in oblate spheroidal coordinates. When solving this equation, , by the method of separation of variables, , with:
In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.
References
- Notes
- ↑ Flammer, C. (1957). Spheroidal wave functions. Stanford University Press Stanford, Calif.
- Bibliography
- C. Niven On the Conduction of Heat in Ellipsoids of Revolution. Philosophical transactions of the Royal Society of London, v. 171 p. 117 (1880)
- M. Abramowitz and I. Stegun, Handbook of Mathematical function (US Gov. Printing Office, Washington DC, 1964)
- Volkmer, H. (2010), "Spheroidal wave function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248