A (symmetric) n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base. An n-gonal bipyramid has 2n triangle faces, 3n edges, and 2 + n vertices.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

In geometry, square pyramid is a pyramid that has four triangles, and one square as the base, from which there are five faces in total. As for an apex that is perpendicularly above the center of the base, it is a right square pyramid that has four isosceles triangles; otherwise, it is an oblique square pyramid. When all the edges have the same length, the four triangular faces become equilateral, an equilateral square pyramid.

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. An object that is not chiral is said to be achiral.

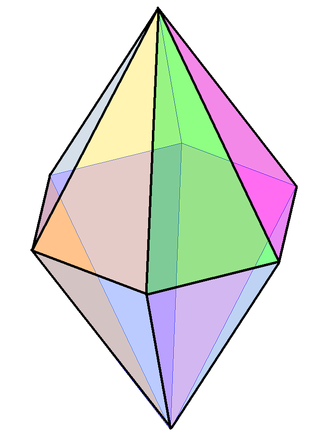
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.

The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

In geometry, a disphenoid is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron, sphenoid, bisphenoid, isosceles tetrahedron, equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".


















