
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For any positive integer
In mathematics, the Laplace transform, named after its inventor Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms differential equations into algebraic equations and convolution into multiplication.
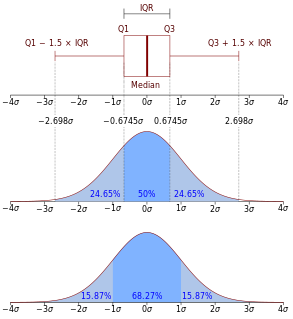
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two signals is the pointwise product of their Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain. Versions of the convolution theorem are true for various Fourier-related transforms. Let and be two functions with convolution .

In mathematics, a Fourier series is a periodic function composed of harmonically related sinusoids, combined by a weighted summation. With appropriate weights, one cycle of the summation can be made to approximate an arbitrary function in that interval. As such, the summation is a synthesis of another function. The discrete-time Fourier transform is an example of Fourier series. The process of deriving the weights that describe a given function is a form of Fourier analysis. For functions on unbounded intervals, the analysis and synthesis analogies are Fourier transform and inverse transform.
In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form
The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples of the original function's Fourier transform. And conversely, the periodic summation of a function's Fourier transform is completely defined by discrete samples of the original function. The Poisson summation formula was discovered by Siméon Denis Poisson and is sometimes called Poisson resummation.

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function :
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of values.

In mathematics, a Dirac comb is a periodic tempered distribution constructed from Dirac delta functions

In quantum field theory, the LSZ reduction formula is a method to calculate S-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann.
Linear time-invariant theory, commonly known as LTI system theory, investigates the response of a linear and time-invariant system to an arbitrary input signal. Trajectories of these systems are commonly measured and tracked as they move through time, but in applications like image processing and field theory, the LTI systems also have trajectories in spatial dimensions. Thus, these systems are also called linear translation-invariant to give the theory the most general reach. In the case of generic discrete-time systems, linear shift-invariant is the corresponding term. A good example of LTI systems are electrical circuits that can be made up of resistors, capacitors, and inductors.. It has been used in applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas.
The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product






























