 | This article may be too technical for most readers to understand.(December 2021) |
Stationary Subspace Analysis (SSA) [1] in statistics is a blind source separation algorithm which factorizes a multivariate time series into stationary and non-stationary components.
In many settings, the measured time series contains contributions from various underlying sources that cannot be measured directly. For instance, in EEG analysis, the electrodes on the scalp record the activity of a large number of sources located inside the brain. [2] These sources can be stationary or non-stationary, but they are not discernible in the electrode signals, which are a mixture of these sources. SSA allows the separation of the stationary from the non-stationary sources in an observed time series.
According to the SSA model, [1] the observed multivariate time series is assumed to be generated as a linear superposition of stationary sources and non-stationary sources ,
where is an unknown but time-constant mixing matrix; and are the basis of the stationary and non-stationary subspace respectively.
Given samples from the time series , the aim of Stationary Subspace Analysis is to estimate the inverse mixing matrix separating the stationary from non-stationary sources in the mixture .
The true stationary sources are identifiable (up to a linear transformation) and the true non-stationary subspace is identifiable. The true non-stationary sources and the true stationary subspace cannot be identified, because arbitrary contributions from the stationary sources do not change the non-stationary nature of a non-stationary source. [1]
Stationary subspace analysis has been successfully applied to Brain-computer interfacing, [3] computer vision [4] and temporal segmentation. There are variants of the SSA problem that can be solved analytically in closed form, without numerical optimization. [5]
In mathematics, a Lie algebra is a vector space together with an operation called the Lie bracket, an alternating bilinear map , that satisfies the Jacobi identity. The vector space together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative.
Source separation, blind signal separation (BSS) or blind source separation, is the separation of a set of source signals from a set of mixed signals, without the aid of information about the source signals or the mixing process. It is most commonly applied in digital signal processing and involves the analysis of mixtures of signals; the objective is to recover the original component signals from a mixture signal. The classical example of a source separation problem is the cocktail party problem, where a number of people are talking simultaneously in a room, and a listener is trying to follow one of the discussions. The human brain can handle this sort of auditory source separation problem, but it is a difficult problem in digital signal processing.
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.
In mathematics, the adjoint representation of a Lie group G is a way of representing the elements of the group as linear transformations of the group's Lie algebra, considered as a vector space. For example, if G is , the Lie group of real n-by-n invertible matrices, then the adjoint representation is the group homomorphism that sends an invertible n-by-n matrix to an endomorphism of the vector space of all linear transformations of defined by: .
In linear algebra, a Jordan normal form, also known as a Jordan canonical form or JCF, is an upper triangular matrix of a particular form called a Jordan matrix representing a linear operator on a finite-dimensional vector space with respect to some basis. Such a matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal, and with identical diagonal entries to the left and below them.
In mathematics and statistics, a stationary process is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Consequently, parameters such as mean and variance also do not change over time. To get an intuition of stationarity, one can imagine a frictionless pendulum. It swings back and forth in an oscillatory motion, yet the amplitude and frequency remain constant. Although the pendulum is moving, the process is stationary as its "statistics" are constant. However, if a force were to be applied to the pendulum, either the frequency or amplitude would change, thus making the process non-stationary.
In mathematics, the Heisenberg group, named after Werner Heisenberg, is the group of 3×3 upper triangular matrices of the form
In linear algebra and functional analysis, a projection is a linear transformation from a vector space to itself such that . That is, whenever is applied twice to any vector, it gives the same result as if it were applied once. It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents. This is done by assuming that the subcomponents are, potentially, non-Gaussian signals and that they are statistically independent from each other. ICA is a special case of blind source separation. A common example application is the "cocktail party problem" of listening in on one person's speech in a noisy room.
In statistics, a vector of random variables is heteroscedastic if the variability of the random disturbance is different across elements of the vector. Here, variability could be quantified by the variance or any other measure of statistical dispersion. Thus heteroscedasticity is the absence of homoscedasticity. A typical example is the set of observations of income in different cities.
In mathematics, a unipotent elementr of a ring R is one such that r − 1 is a nilpotent element; in other words, (r − 1)n is zero for some n.
In probability theory and statistics, a copula is a multivariate cumulative distribution function for which the marginal probability distribution of each variable is uniform on the interval [0, 1]. Copulas are used to describe/model the dependence (inter-correlation) between random variables. Their name, introduced by applied mathematician Abe Sklar in 1959, comes from the Latin for "link" or "tie", similar but unrelated to grammatical copulas in linguistics. Copulas have been used widely in quantitative finance to model and minimize tail risk and portfolio-optimization applications.
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by , is the factor by which the eigenvector is scaled.
In mathematics, in the area of numerical analysis, Galerkin methods, named after the Russian mathematician Boris Galerkin, convert a continuous operator problem, such as a differential equation, commonly in a weak formulation, to a discrete problem by applying linear constraints determined by finite sets of basis functions.
In mathematics, a Lie algebra is solvable if its derived series terminates in the zero subalgebra. The derived Lie algebra of the Lie algebra is the subalgebra of , denoted
In mathematics, Fourier–Bessel series is a particular kind of generalized Fourier series based on Bessel functions.
In time series analysis, singular spectrum analysis (SSA) is a nonparametric spectral estimation method. It combines elements of classical time series analysis, multivariate statistics, multivariate geometry, dynamical systems and signal processing. Its roots lie in the classical Karhunen (1946)–Loève spectral decomposition of time series and random fields and in the Mañé (1981)–Takens (1981) embedding theorem. SSA can be an aid in the decomposition of time series into a sum of components, each having a meaningful interpretation. The name "singular spectrum analysis" relates to the spectrum of eigenvalues in a singular value decomposition of a covariance matrix, and not directly to a frequency domain decomposition.
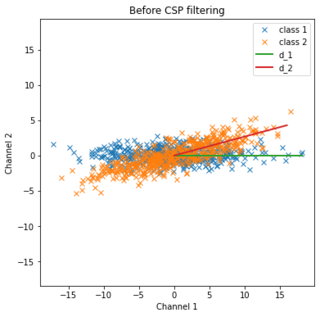
Common spatial pattern (CSP) is a mathematical procedure used in signal processing for separating a multivariate signal into additive subcomponents which have maximum differences in variance between two windows.
Brain connectivity estimators represent patterns of links in the brain. Connectivity can be considered at different levels of the brain's organisation: from neurons, to neural assemblies and brain structures. Brain connectivity involves different concepts such as: neuroanatomical or structural connectivity, functional connectivity and effective connectivity.
jblas is a linear algebra library, created by Mikio Braun, for the Java programming language built upon BLAS and LAPACK. Unlike most other Java linear algebra libraries, jblas is designed to be used with native code through the Java Native Interface (JNI) and comes with precompiled binaries. When used on one of the targeted architectures, it will automatically select the correct binary to use and load it. This allows it to be used out of the box and avoid a potentially tedious compilation process. jblas provides an easier to use high level API on top of the archaic API provided by BLAS and LAPACK, removing much of the tediousness.
