Strand sort

Last updated
Strand Sort Animation StrandSort.gif
Strand Sort Animation

Strand sort is a recursive sorting algorithm that sorts items of a list into increasing order. It has O(n2) worst time complexity which occurs when the input list is reverse sorted. [1] It has a best case time complexity of O(n) which occurs when the input is a list that is already sorted.[ citation needed ]

Contents

The algorithm first moves the first element of a list into a sub-list. [1] It then compares the last element in the sub-list to each subsequent element in the original list. [1] Once there is an element in the original list that is greater than the last element in the sub-list, the element is removed from the original list and added to the sub-list. [1] This process continues until the last element in the sub-list is compared to the remaining elements in the original list. [1] The sub-list is then merged into a new list. [1] Repeat this process and merge all sub-lists until all elements are sorted. [1] This algorithm is called strand sort because there are strands of sorted elements within the unsorted elements that are removed one at a time. [1] This algorithm is also used in J Sort for fewer than 40 elements. [2]

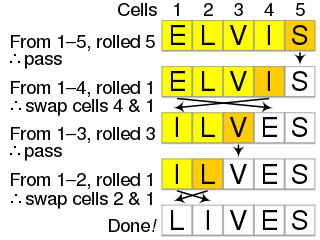
Example

This example is based on the description of the algorithm provided in the book, IT Enabled Practices and Emerging Management Paradigms. [1]

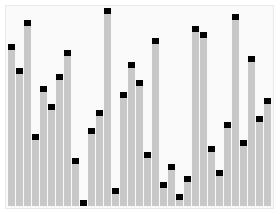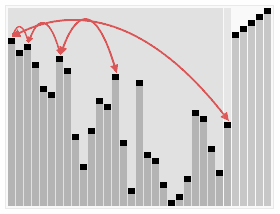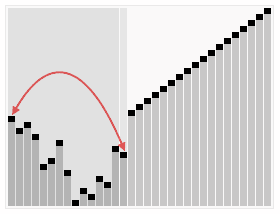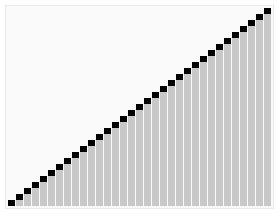
Step 1: Start with a list of numbers: {5, 1, 4, 2, 0, 9, 6, 3, 8, 7 }

Step 2: Next move the first element of the list into a new sub-list:  sub-list contains {5}

Step 3: Then iterate through the original list and compare each number to 5 until there is a number greater than 5.

Step 4: Now compare 9 with the remaining elements in the original list until there is a number greater than 9.  

Step 5: Now there are no more elements to compare 9 to so merge the sub-list into a new list, called solution-list.

After step 5, the original list contains {1, 4, 2, 0, 6, 3, 8, 7}

The sub-list is empty, and the solution list contains {5, 9}

Step 6: Move the first element of the original list into sub-list: sub-list contains {1}

Step 7: Iterate through the original list and compare each number to 1 until there is a number greater than 1.

Step 8: Now compare 4 with the remaining elements in the original list until there is a number greater than 4.

Step 9: Now compare 6 with the remaining elements in the original list until there is a number greater than 6.  

Step 10: Now compare 8 with the remaining elements in the original list until there is a number greater than 8.

Step 11: Since there are no more elements in the original list to compare {8} to, the sub-list is merged with the solution list. Now the original list contains {2, 0, 3, 7}, the sub-list is empty and the solution-list contains: {1, 4, 5, 6, 8, 9}.

Step 12:  Move the first element of the original list into sub-list. Sub-list contains {2}

Step 13: Iterate through the original list and compare each number to 2 until there is a number greater than 2.

Step 14: Now compare 3 with the remaining elements in the original list until there is a number greater than 3.

Step 15: Since there are no more elements in the original list to compare {7} to, the sub-list is merged with the solution list. The original list now contains {0}, the sub-list is empty, and solution list contains: {1, 2, 3, 4, 5, 6, 7, 8, 9}.

Step 16:  Move the first element of the original list into sub-list. Sub-list contains {0}.

Step 17:  Since the original list is now empty, the sub-list is merged with the solution list. The solution list now contains: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. There are now no more elements in the original list, and all of the elements in the solution list have successfully been sorted into increasing numerical order.

Implementation

Since Strand Sort requires many insertions and deletions, it is best to use a linked list when implementing the algorithm. [3] Linked lists require constant time for both insertions and removals of elements using iterators. The time to traverse through the linked list is directly related to the input size of the list. [4] The following implementation is done in Java 8 and is based on the description of the algorithm from the book, IT Enabled Practices and Emerging Management Paradigms. [1] 

packagestrandSort;importjava.util.*;publicclassstrandSort{staticLinkedList<Integer>solList=newLinkedList<Integer>();staticintk=0;/**  * This is a recursive Strand Sort method. It takes in a linked list of  * integers as its parameter. It first checks the base case to see if the  * linked list is empty. Then proceeds to the Strand sort algorithm until  * the linked list is empty.  *   * @param origList:  *            a linked list of integers  */publicstaticvoidstrandSortIterative(LinkedList<Integer>origList){// Base Caseif(origList.isEmpty()){return;}else{// Create the subList and add the first element of// The original linked list to the sublist.// Then remove the first element from the original list.LinkedList<Integer>subList=newLinkedList<Integer>();subList.add(origList.getFirst());origList.removeFirst();// Iterate through the original list, checking if any elements are// Greater than the element in the sub list.intindex=0;for(intj=0;j<origList.size();j++){if(origList.get(j)>subList.get(index)){subList.add(origList.get(j));origList.remove(j);j=j-1;index=index+1;}}// Merge sub-list into solution list.// There are two cases for this step/// Case 1: The first recursive call, add all of the elements to the// solution list in sequential orderif(k==0){for(inti=0;i<subList.size();i++){solList.add(subList.get(i));k=k+1;}}// Case 2: After the first recursive call, // merge the sub-list with the solution list.// This works by comparing the greatest element in the sublist (which is always the last element)// with the first element in the solution list. else{intsubEnd=subList.size()-1;intsolStart=0;while(!subList.isEmpty()){if(subList.get(subEnd)>solList.get(solStart)){solStart++;}else{solList.add(solStart,subList.get(subEnd));subList.remove(subEnd);subEnd--;solStart=0;}}}strandSortIterative(origList);}}publicstaticvoidmain(String[]args){// Create a new linked list of IntegersLinkedList<Integer>origList=newLinkedList<Integer>();// Add the following integers to the linked list: {5, 1, 4, 2, 0, 9, 6, 3, 8, 7}origList.add(5);origList.add(1);origList.add(4);origList.add(2);origList.add(0);origList.add(9);origList.add(6);origList.add(3);origList.add(8);origList.add(7);strandSortIterative(origList);// Print out the solution listfor(inti=0;i<solList.size();i++){System.out.println(solList.get(i));}}}

Related Research Articles

Binary search algorithm Search algorithm finding the position of a target value within a sorted array

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

Heapsort A sorting algorithm which uses the heap data structure

In computer science, heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step.

Heap (data structure) Computer science data structure

In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.

Insertion sort Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains: data, and a reference to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that access time is linear. Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.

Merge algorithms are a family of algorithms that take multiple sorted lists as input and produce a single list as output, containing all the elements of the inputs lists in sorted order. These algorithms are used as subroutines in various sorting algorithms, most famously merge sort.

In computer science, selection sort is an in-place comparison sorting algorithm. It has an O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.

The subset sum problem (SSP) is a decision problem in computer science. In its most general formulation, there is a multiset of integers and a target-sum , and the question is to decide whether any subset of the integers sum to precisely . The problem is known to be NP-complete. Moreover, some restricted variants of it are NP-complete too, for example:

In object-oriented programming, the iterator pattern is a design pattern in which an iterator is used to traverse a container and access the container's elements. The iterator pattern decouples algorithms from containers; in some cases, algorithms are necessarily container-specific and thus cannot be decoupled.

In computer science, a set is an abstract data type that can store unique values, without any particular order. It is a computer implementation of the mathematical concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set.

Bead sort, also called gravity sort, is a natural sorting algorithm, developed by Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen in 2002, and published in The Bulletin of the European Association for Theoretical Computer Science. Both digital and analog hardware implementations of bead sort can achieve a sorting time of O(n); however, the implementation of this algorithm tends to be significantly slower in software and can only be used to sort lists of positive integers. Also, it would seem that even in the best case, the algorithm requires O(n2) space.

Quicksort Divide and conquer sorting algorithm

Quicksort is an in-place sorting algorithm. Developed by British computer scientist Tony Hoare in 1959 and published in 1961, it is still a commonly used algorithm for sorting. When implemented well, it can be somewhat faster than merge sort and about two or three times faster than heapsort.

In computer programming, a sentinel value is a special value in the context of an algorithm which uses its presence as a condition of termination, typically in a loop or recursive algorithm.

Recursion (computer science) Use of functions that call themselves

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.

The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.

sort is a generic function in the C++ Standard Library for doing comparison sorting. The function originated in the Standard Template Library (STL).

In computer science, adaptive heap sort is a comparison-based sorting algorithm of the adaptive sort family. It is a variant of heap sort that performs better when the data contains existing order. Published by Christos Levcopoulos and Ola Petersson in 1992, the algorithm utilizes a new measure of presortedness, Osc, as the number of oscillations. Instead of putting all the data into the heap as the traditional heap sort did, adaptive heap sort only take part of the data into the heap so that the run time will reduce significantly when the presortedness of the data is high.

Fisher–Yates shuffle Algorithm for generating a random permutation of a finite set

The Fisher–Yates shuffle is an algorithm for generating a random permutation of a finite sequence—in plain terms, the algorithm shuffles the sequence. The algorithm effectively puts all the elements into a hat; it continually determines the next element by randomly drawing an element from the hat until no elements remain. The algorithm produces an unbiased permutation: every permutation is equally likely. The modern version of the algorithm is efficient: it takes time proportional to the number of items being shuffled and shuffles them in place.

In computing, sequence containers refer to a group of container class templates in the standard library of the C++ programming language that implement storage of data elements. Being templates, they can be used to store arbitrary elements, such as integers or custom classes. One common property of all sequential containers is that the elements can be accessed sequentially. Like all other standard library components, they reside in namespace std.

In computer science, k-way merge algorithms or multiway merges are a specific type of sequence merge algorithms that specialize in taking in k sorted lists and merging them into a single sorted list. These merge algorithms generally refer to merge algorithms that take in a number of sorted lists greater than two. Two-way merges are also referred to as binary merges.

Bucket queue Data structure for integer priorities

A bucket queue is a data structure that implements the priority queue abstract data type: it maintains a dynamic collection of elements with numerical priorities and allows quick access to the element with minimum priority. In the bucket queue, the priorities must be integers, and it is particularly suited to applications in which the priorities have a small range. A bucket queue has the form of an array of buckets: an array data structure, indexed by the priorities, whose cells contain collections of items with the same priority as each other. With this data structure, insertion of elements and changes of their priority take constant time. Searching for and removing the minimum-priority element takes time proportional to the number of buckets or, by maintaining a pointer to the most recently found bucket, in time proportional to the difference in priorities between successive operations.

References

  1. 1 2 3 4 5 6 7 8 9 10 IT enabled practices and emerging management paradigms. Gupta, I. C. (Ishwar Chandra), 1946-, Jaroliya, Deepak., Prestige Institute of Management and Research. (1st ed.). Indore: Prestige Institute of Management and Research. 2008. ISBN   9788174466761. OCLC   641462443.{{cite book}}: CS1 maint: others (link)
  2. ↑ Sudipta., Mukherjee (2008). Data structures using C : 1000 problems and solutions. New Delhi: Tata McGraw-Hill. ISBN   9780070667655. OCLC   311311576.
  3. ↑ "strand sort". xlinux.nist.gov. Retrieved 2018-11-06.
  4. ↑ "LinkedLists". www.cs.cmu.edu. Retrieved 2018-11-06.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.