Related Research Articles
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
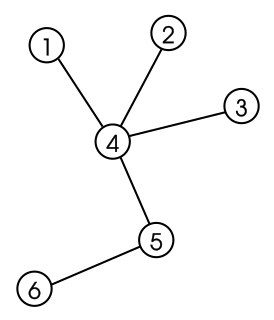
In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.
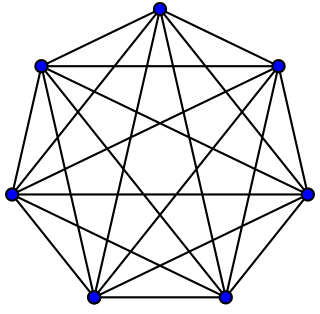
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.

In bioinformatics, a sequence alignment is a way of arranging the sequences of DNA, RNA, or protein to identify regions of similarity that may be a consequence of functional, structural, or evolutionary relationships between the sequences. Aligned sequences of nucleotide or amino acid residues are typically represented as rows within a matrix. Gaps are inserted between the residues so that identical or similar characters are aligned in successive columns. Sequence alignments are also used for non-biological sequences, such as calculating the distance cost between strings in a natural language or in financial data.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
Electronic design automation (EDA), also referred to as electronic computer-aided design (ECAD), is a category of software tools for designing electronic systems such as integrated circuits and printed circuit boards. The tools work together in a design flow that chip designers use to design and analyze entire semiconductor chips. Since a modern semiconductor chip can have billions of components, EDA tools are essential for their design; this article in particular describes EDA specifically with respect to integrated circuits (ICs).

Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

Solid modeling is a consistent set of principles for mathematical and computer modeling of three-dimensional shapes (solids). Solid modeling is distinguished from related areas of geometric modeling and computer graphics, such as 3D modeling, by its emphasis on physical fidelity. Together, the principles of geometric and solid modeling form the foundation of 3D-computer-aided design and in general support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act.
A spatial database is a general-purpose database that has been enhanced to include spatial data that represents objects defined in a geometric space, along with tools for querying and analyzing such data. Most spatial databases allow the representation of simple geometric objects such as points, lines and polygons. Some spatial databases handle more complex structures such as 3D objects, topological coverages, linear networks, and triangulated irregular networks (TINs). While typical databases have developed to manage various numeric and character types of data, such databases require additional functionality to process spatial data types efficiently, and developers have often added geometry or feature data types. The Open Geospatial Consortium (OGC) developed the Simple Features specification and sets standards for adding spatial functionality to database systems. The SQL/MM Spatial ISO/IEC standard is a part the SQL/MM multimedia standard and extends the Simple Features standard with data types that support circular interpolations.

In integrated circuit design, physical design is a step in the standard design cycle which follows after the circuit design. At this step, circuit representations of the components of the design are converted into geometric representations of shapes which, when manufactured in the corresponding layers of materials, will ensure the required functioning of the components. This geometric representation is called integrated circuit layout. This step is usually split into several sub-steps, which include both design and verification and validation of the layout.

Kurt Mehlhorn is a German theoretical computer scientist. He has been a vice president of the Max Planck Society and is director of the Max Planck Institute for Computer Science.
Geometric data analysis comprises geometric aspects of image analysis, pattern analysis and shape analysis and the approach of multivariate statistics that treats arbitrary data sets as clouds of points in n-dimensional space. This includes topological data analysis, cluster analysis, inductive data analysis, correspondence analysis, multiple correspondence analysis, principal components analysis and fr:Iconographie des corrélations.
In statistics, combinatorial data analysis (CDA) is the study of data sets where the order in which objects are arranged is important. CDA can be used either to determine how well a given combinatorial construct reflects the observed data, or to search for a suitable combinatorial construct that does fit the data.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.
In combinatorial mathematics and theoretical computer science, heavy path decomposition is a technique for decomposing a rooted tree into a set of paths. In a heavy path decomposition, each non-leaf node selects one "heavy edge", the edge to the child that has the greatest number of descendants. The selected edges form the paths of the decomposition.
References
- ↑ Brigitte Le Roux; Henry Rouanet (2004). Geometric Data Analysis: from Correspondence Analysis to Structured Data Analysis. Springer. ISBN 978-1402022357.
- ↑ Lawrence J. Hubert, Phipps Arabie, Jacqueline Meulman (2001). Combinatorial Data Analysis: Optimization by Dynamic Programming. SIAM. ISBN 978-0898714784.
{{cite book}}: CS1 maint: multiple names: authors list (link)