In mathematics, the Laplace transform, named after Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable .
In propositional logic, modus ponens, also known as modus ponendo ponens, implication elimination, or affirming the antecedent, is a deductive argument form and rule of inference. It can be summarized as "P implies Q.P is true. Therefore, Q must also be true."
In propositional logic, modus tollens (MT), also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference. Modus tollens is a mixed hypothetical syllogism that takes the form of "If P, then Q. Not Q. Therefore, not P." It is an application of the general truth that if a statement is true, then so is its contrapositive. The form shows that inference from P implies Q to the negation of Q implies the negation of P is a valid argument.

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
Bayes' theorem gives a mathematical rule for inverting conditional probabilities, allowing us to find the probability of a cause given its effect. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately by conditioning it relative to their age, rather than assuming that the individual is typical of the population as a whole. Based on Bayes law both the prevalence of a disease in a given population and the error rate of an infectious disease test have to be taken into account to evaluate the meaning of a positive test result correctly and avoid the base-rate fallacy.

Abductive reasoning is a form of logical inference that seeks the simplest and most likely conclusion from a set of observations. It was formulated and advanced by American philosopher and logician Charles Sanders Peirce beginning in the latter half of the 19th century.

The theory of belief functions, also referred to as evidence theory or Dempster–Shafer theory (DST), is a general framework for reasoning with uncertainty, with understood connections to other frameworks such as probability, possibility and imprecise probability theories. First introduced by Arthur P. Dempster in the context of statistical inference, the theory was later developed by Glenn Shafer into a general framework for modeling epistemic uncertainty—a mathematical theory of evidence. The theory allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence.
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state that has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator arise in the quantum theory of a wide range of physical systems. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well. The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be related to classical solutions by a particle oscillating with an amplitude equivalent to the displacement.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.

In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.
In logic, a truth function is a function that accepts truth values as input and produces a unique truth value as output. In other words: the input and output of a truth function are all truth values; a truth function will always output exactly one truth value, and inputting the same truth value(s) will always output the same truth value. The typical example is in propositional logic, wherein a compound statement is constructed using individual statements connected by logical connectives; if the truth value of the compound statement is entirely determined by the truth value(s) of the constituent statement(s), the compound statement is called a truth function, and any logical connectives used are said to be truth functional.
A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state.
Possibility theory is a mathematical theory for dealing with certain types of uncertainty and is an alternative to probability theory. It uses measures of possibility and necessity between 0 and 1, ranging from impossible to possible and unnecessary to necessary, respectively. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic. Didier Dubois and Henri Prade further contributed to its development. Earlier, in the 1950s, economist G. L. S. Shackle proposed the min/max algebra to describe degrees of potential surprise.
Probability theory and statistics have some commonly used conventions, in addition to standard mathematical notation and mathematical symbols.
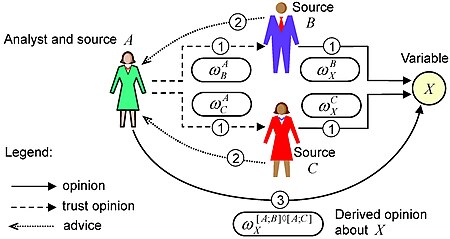
Probabilistic logic involves the use of probability and logic to deal with uncertain situations. Probabilistic logic extends traditional logic truth tables with probabilistic expressions. A difficulty of probabilistic logics is their tendency to multiply the computational complexities of their probabilistic and logical components. Other difficulties include the possibility of counter-intuitive results, such as in case of belief fusion in Dempster–Shafer theory. Source trust and epistemic uncertainty about the probabilities they provide, such as defined in subjective logic, are additional elements to consider. The need to deal with a broad variety of contexts and issues has led to many different proposals.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In logic and mathematics, contraposition, or transposition, refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as § Proof by contrapositive. The contrapositive of a statement has its antecedent and consequent inverted and flipped.

In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is A and the event B is known or assumed to have occurred, "the conditional probability of A given B", or "the probability of A under the condition B", is usually written as P(A|B) or occasionally PB(A). This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): .
Vasiliev equations are formally consistent gauge invariant nonlinear equations whose linearization over a specific vacuum solution describes free massless higher-spin fields on anti-de Sitter space. The Vasiliev equations are classical equations and no Lagrangian is known that starts from canonical two-derivative Frønsdal Lagrangian and is completed by interactions terms. There is a number of variations of Vasiliev equations that work in three, four and arbitrary number of space-time dimensions. Vasiliev's equations admit supersymmetric extensions with any number of super-symmetries and allow for Yang–Mills gaugings. Vasiliev's equations are background independent, the simplest exact solution being anti-de Sitter space. It is important to note that locality is not properly implemented and the equations give a solution of certain formal deformation procedure, which is difficult to map to field theory language. The higher-spin AdS/CFT correspondence is reviewed in Higher-spin theory article.
In set theory and logic, Buchholz's ID hierarchy is a hierarchy of subsystems of first-order arithmetic. The systems/theories are referred to as "the formal theories of ν-times iterated inductive definitions". IDν extends PA by ν iterated least fixed points of monotone operators.