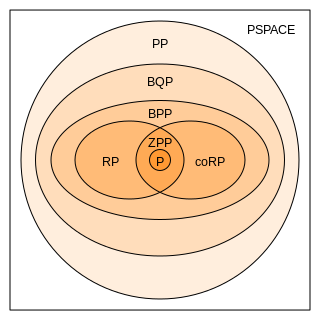
Sulston score

Last updated October 05, 2024

The Sulston score is an equation used in DNA mapping to numerically assess the likelihood that a given "fingerprint" similarity between two DNA clones is merely a result of chance. Used as such, it is a test of statistical significance. That is, low values imply that similarity is significant, suggesting that two DNA clones overlap one another and that the given similarity is not just a chance event. The name is an eponym that refers to John Sulston by virtue of his being the lead author of the paper that first proposed the equation's use.^[1]

The overlap problem in mapping

Each clone in a DNA mapping project has a "fingerprint", i.e. a set of DNA fragment lengths inferred from (1) enzymatically digesting the clone, (2) separating these fragments on a gel, and (3) estimating their lengths based on gel location. For each pairwise clone comparison, one can establish how many lengths from each set match-up. Cases having at least 1 match indicate that the clones might overlap because matches may represent the same DNA. However, the underlying sequences for each match are not known. Consequently, two fragments whose lengths match may still represent different sequences. In other words, matches do not conclusively indicate overlaps. The problem is instead one of using matches to probabilistically classify overlap status.

Mathematical scores in overlap assessment

Biologists have used a variety of means (often in combination) to discern clone overlaps in DNA mapping projects. While many are biological, i.e. looking for shared markers, others are basically mathematical, usually adopting probabilistic and/or statistical approaches.

Sulston score exposition

The Sulston score is rooted in the concepts of Bernoulli and binomial processes, as follows. Consider two clones, $\alpha$ and $\beta$ , having $m$ and $n$ measured fragment lengths, respectively, where $m\geq n$ . That is, clone $\alpha$ has at least as many fragments as clone $\beta$ , but usually more. The Sulston score is the probability that at least $h$ fragment lengths on clone $\beta$ will be matched by any combination of lengths on $\alpha$ . Intuitively, we see that, at most, there can be $n$ matches. Thus, for a given comparison between two clones, one can measure the statistical significance of a match of $h$ fragments, i.e. how likely it is that this match occurred simply as a result of random chance. Very low values would indicate a significant match that is highly unlikely to have arisen by pure chance, while higher values would suggest that the given match could be just a coincidence.

Derivation of the Sulston Score

One of the basic assumptions is that fragments are uniformly distributed on a gel, i.e. a fragment has an equal likelihood of appearing anywhere on the gel. Since gel position is an indicator of fragment length, this assumption is equivalent to presuming that the fragment lengths are uniformly distributed. The measured location of any fragment

x

, has an associated error tolerance of

\pm t

, so that its true location is only known to lie within the segment

x\pm t

.

In what follows, let us refer to individual fragment lengths simply as lengths. Consider a specific length $j$ on clone $\beta$ and a specific length $i$ on clone $\alpha$ . These two lengths are arbitrarily selected from their respective sets $i\in \{1,2,\dots ,m\}$ and $j\in \{1,2,\dots ,n\}$ . We assume that the gel location of fragment $j$ has been determined and we want the probability of the event $E_{ij}$ that the location of fragment $i$ will match that of $j$ . Geometrically, $i$ will be declared to match $j$ if it falls inside the window of size $2t$ around $j$ . Since fragment $i$ could occur anywhere in the gel of length $G$ , we have $P\langle E_{ij}\rangle =2t/G$ . The probability that $i$ does not match $j$ is simply the complement, i.e. $P\langle E_{i,j}^{C}\rangle =1-2t/G$ , since it must either match or not match.

Now, let us expand this to compute the probability that no length on clone $\alpha$ matches the single particular length $j$ on clone $\beta$ . This is simply the intersection of all individual trials $i\in \{1,2,\dots ,m\}$ where the event $E_{i,j}^{C}$ occurs, i.e. $P\langle E_{1,j}^{C}\cap E_{2,j}^{C}\cap \cdots \cap E_{m,j}^{C}\rangle$ . This can be restated verbally as: length 1 on clone $\alpha$ does not match length $j$ on clone $\beta$ and length 2 does not match length $j$ and length 3 does not match, etc. Since each of these trials is assumed to be independent, the probability is simply

P\langle E_{1,j}^{C}\rangle \times P\langle E_{2,j}^{C}\rangle \times \cdots \times P\langle E_{m,j}^{C}\rangle =\left(1-2t/G\right)^{m}.

Of course, the actual event of interest is the complement: i.e. there is not "no matches". In other words, the probability of one or more matches is $p=1-\left(1-2t/G\right)^{m}$ . Formally, $p$ is the probability that at least one band on clone $\alpha$ matches band $j$ on clone $\beta$ .

This event is taken as a Bernoulli trial having a "success" (matching) probability of $p$ for band $j$ . However, we want to describe the process over all the bands on clone $\beta$ . Since $p$ is constant, the number of matches is distributed binomially. Given $h$ observed matches, the Sulston score $S$ is simply the probability of obtaining at least $h$ matches by chance according to

S=\sum _{j=h}^{n}C_{n,j}p^{j}(1-p)^{n-j},

where $C_{n,j}$ are binomial coefficients.

Mathematical refinement

In a 2005 paper,^[2] Michael Wendl gave an example showing that the assumption of independent trials is not valid. So, although the traditional Sulston score does indeed represent a probability distribution, it is not actually the distribution characteristic of the fingerprint problem. Wendl went on to give the general solution for this problem in terms of the Bell polynomials, showing the traditional score overpredicts P-values by orders of magnitude. (P-values are very small in this problem, so we are talking, for example, about probabilities on the order of 10×10⁻¹⁴ versus 10×10⁻¹², the latter Sulston value being 2 orders of magnitude too high.) This solution provides a basis for determining when a problem has sufficient information content to be treated by the probabilistic approach and is also a general solution to the birthday problem of 2 types.

A disadvantage of the exact solution is that its evaluation is computationally intensive and, in fact, is not feasible for comparing large clones.^[2] Some fast approximations for this problem have been proposed.^[3]

Related Research Articles

In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.

The Post correspondence problem is an undecidable decision problem that was introduced by Emil Post in 1946. Because it is simpler than the halting problem and the Entscheidungsproblem it is often used in proofs of undecidability.

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or in terms of two positive parameters, denoted by alpha (α) and beta (β), that appear as exponents of the variable and its complement to 1, respectively, and control the shape of the distribution.

In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:

With a shape parameter $k$ and a scale parameter $θ$
With a shape parameter $and an inverse scale parameter ⁠ ⁠, called a rate parameter.$

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

In statistics, a confidence region is a multi-dimensional generalization of a confidence interval. It is a set of points in an n-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur.

A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state.

The expectiminimax algorithm is a variation of the minimax algorithm, for use in artificial intelligence systems that play two-player zero-sum games, such as backgammon, in which the outcome depends on a combination of the player's skill and chance elements such as dice rolls. In addition to "min" and "max" nodes of the traditional minimax tree, this variant has "chance" nodes, which take the expected value of a random event occurring. In game theory terms, an expectiminimax tree is the game tree of an extensive-form game of perfect, but incomplete information.

Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.

A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the states of the Markov process represents one of the phases.

In natural language processing, latent Dirichlet allocation (LDA) is a Bayesian network for modeling automatically extracted topics in textual corpora. The LDA is an example of a Bayesian topic model. In this, observations are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics.

In computational complexity theory, PostBQP is a complexity class consisting of all of the computational problems solvable in polynomial time on a quantum Turing machine with postselection and bounded error.

In probability theory, Dirichlet processes are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose range is itself a set of probability distributions. It is often used in Bayesian inference to describe the prior knowledge about the distribution of random variables—how likely it is that the random variables are distributed according to one or another particular distribution.

<span class="mw-page-title-main">Great ellipse</span> Ellipse on a spheroid centered on its origin

A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of a spheroid and centered on the origin, or the curve formed by intersecting the spheroid by a plane through its center. For points that are separated by less than about a quarter of the circumference of the earth, about $, the length of the great ellipse connecting the points is close to the geodesic distance. The great ellipse therefore is sometimes proposed as a suitable route for marine navigation. The great ellipse is special case of an earth section path.$

In probability theory, Robbins' problem of optimal stopping, named after Herbert Robbins, is sometimes referred to as the fourth secretary problem or the problem of minimizing the expected rank with full information.

Let X₁, ..., X_n be independent, identically distributed random variables, uniform on [0, 1]. We observe the X_k's sequentially and must stop on exactly one of them. No recall of preceding observations is permitted. What stopping rule minimizes the expected rank of the selected observation, and what is its corresponding value?

DNA sequencing theory is the broad body of work that attempts to lay analytical foundations for determining the order of specific nucleotides in a sequence of DNA, otherwise known as DNA sequencing. The practical aspects revolve around designing and optimizing sequencing projects, predicting project performance, troubleshooting experimental results, characterizing factors such as sequence bias and the effects of software processing algorithms, and comparing various sequencing methods to one another. In this sense, it could be considered a branch of systems engineering or operations research. The permanent archive of work is primarily mathematical, although numerical calculations are often conducted for particular problems too. DNA sequencing theory addresses physical processes related to sequencing DNA and should not be confused with theories of analyzing resultant DNA sequences, e.g. sequence alignment. Publications sometimes do not make a careful distinction, but the latter are primarily concerned with algorithmic issues. Sequencing theory is based on elements of mathematics, biology, and systems engineering, so it is highly interdisciplinary. The subject may be studied within the context of computational biology.

In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system.

Michael Christopher Wendl is a mathematician and biomedical engineer who has worked on DNA sequencing theory, covering and matching problems in probability, theoretical fluid mechanics, and co-wrote Phred. He was a scientist on the Human Genome Project and has done bioinformatics and biostatistics work in cancer. Wendl is of ethnic German heritage and is the son of the aerospace engineer Michael J. Wendl.

In computational learning theory, Occam learning is a model of algorithmic learning where the objective of the learner is to output a succinct representation of received training data. This is closely related to probably approximately correct (PAC) learning, where the learner is evaluated on its predictive power of a test set.

Non-homogeneous Gaussian regression (NGR) is a type of statistical regression analysis used in the atmospheric sciences as a way to convert ensemble forecasts into probabilistic forecasts. Relative to simple linear regression, NGR uses the ensemble spread as an additional predictor, which is used to improve the prediction of uncertainty and allows the predicted uncertainty to vary from case to case. The prediction of uncertainty in NGR is derived from both past forecast errors statistics and the ensemble spread. NGR was originally developed for site-specific medium range temperature forecasting, but has since also been applied to site-specific medium-range wind forecasting and to seasonal forecasts, and has been adapted for precipitation forecasting. The introduction of NGR was the first demonstration that probabilistic forecasts that take account of the varying ensemble spread could achieve better skill scores than forecasts based on standard model output statistics approaches applied to the ensemble mean.

References

↑ Sulston J, Mallett F, Staden R, Durbin R, Horsnell T, Coulson A (Mar 1988). "Software for genome mapping by fingerprinting techniques". Comput Appl Biosci. 4 (1): 125–32. doi:10.1093/bioinformatics/4.1.125. PMID 2838135.
1 2 Wendl MC (Apr 2005). "Probabilistic assessment of clone overlaps in DNA fingerprint mapping via a priori models". J. Comput. Biol. 12 (3): 283–97. doi:10.1089/cmb.2005.12.283. PMID 15857243.
↑ Wendl MC (2007). "Algebraic correction methods for computational assessment of clone overlaps in DNA fingerprint mapping". BMC Bioinformatics. 8: 127. doi: 10.1186/1471-2105-8-127 . PMC 1868038 . PMID 17442113.