Related Research Articles
A Bézier curve is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation. Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter.
Computer-aided design (CAD) is the use of computers to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve communications through documentation, and to create a database for manufacturing. Designs made through CAD software are helpful in protecting products and inventions when used in patent applications. CAD output is often in the form of electronic files for print, machining, or other manufacturing operations. The terms computer-aided drafting (CAD) and computer-aided design and drafting (CADD) are also used.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive, and for many applications, mathematically convenient.
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings.
Constructive solid geometry is a technique used in solid modeling. Constructive solid geometry allows a modeler to create a complex surface or object by using Boolean operators to combine simpler objects, potentially generating visually complex objects by combining a few primitive ones.
Solid modeling is a consistent set of principles for mathematical and computer modeling of three-dimensional shapes (solids). Solid modeling is distinguished from related areas of geometric modeling and computer graphics, such as 3D modeling, by its emphasis on physical fidelity. Together, the principles of geometric and solid modeling form the foundation of 3D-computer-aided design and in general support the creation, exchange, visualization, animation, interrogation, and annotation of digital models of physical objects.
In computational geometry, the point-in-polygon (PIP) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon. It is a special case of point location problems and finds applications in areas that deal with processing geometrical data, such as computer graphics, computer vision, geographic information systems (GIS), motion planning, and computer-aided design (CAD).
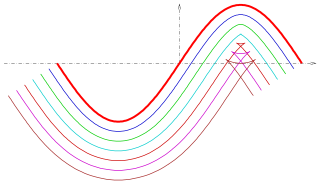
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of parallel (straight) lines. It can also be defined as a curve whose points are at a constant normal distance from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not.
In mathematics, intersection theory is one of the main branches of algebraic geometry, where it gives information about the intersection of two subvarieties of a given variety. The theory for varieties is older, with roots in Bézout's theorem on curves and elimination theory. On the other hand, the topological theory more quickly reached a definitive form.
Geometric modeling is a branch of applied mathematics and computational geometry that studies methods and algorithms for the mathematical description of shapes. The shapes studied in geometric modeling are mostly two- or three-dimensional, although many of its tools and principles can be applied to sets of any finite dimension. Today most geometric modeling is done with computers and for computer-based applications. Two-dimensional models are important in computer typography and technical drawing. Three-dimensional models are central to computer-aided design and manufacturing (CAD/CAM), and widely used in many applied technical fields such as civil and mechanical engineering, architecture, geology and medical image processing.
In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.
Boolean operations on polygons are a set of Boolean operations operating on one or more sets of polygons in computer graphics. These sets of operations are widely used in computer graphics, CAD, and in EDA.
In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.
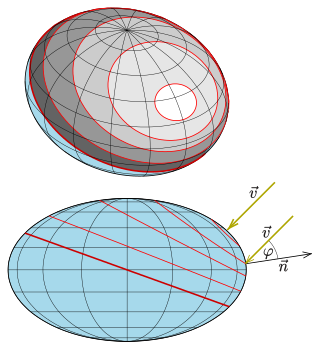
In geometry, an isophote is a curve on an illuminated surface that connects points of equal brightness. One supposes that the illumination is done by parallel light and the brightness b is measured by the following scalar product:
Geometrical design (GD) is a branch of computational geometry. It deals with the construction and representation of free-form curves, surfaces, or volumes and is closely related to geometric modeling. Core problems are curve and surface modelling and representation. GD studies especially the construction and manipulation of curves and surfaces given by a set of points using polynomial, rational, piecewise polynomial, or piecewise rational methods. The most important instruments here are parametric curves and parametric surfaces, such as Bézier curves, spline curves and surfaces. An important non-parametric approach is the level-set method.
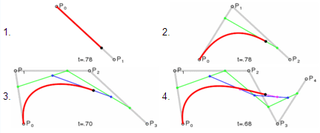
In mathematics, the variation diminishing property of certain mathematical objects involves diminishing the number of changes in sign.
In geometry, an intersection is a point, line, or curve common to two or more objects. The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist. Other types of geometric intersection include:
In geometry, an intersection curve is a curve that is common to two geometric objects. In the simplest case, the intersection of two non-parallel planes in Euclidean 3-space is a line. In general, an intersection curve consists of the common points of two transversally intersecting surfaces, meaning that at any common point the surface normals are not parallel. This restriction excludes cases where the surfaces are touching or have surface parts in common.
References
- ↑ Barnhill, R.; Farin, G.; Jordan, M.; Piper, B. (1987). "Surface/Surface Intersection". Computer Aided Geometric Design. 4 (3): 16.
- ↑ M. Hohmeyer. Robust and Efficient Surface Intersection for Solid Modeling. Report No. UCB/CSD 92/681 May 1992, Computer Science Division (EECS), University of California, Berkeley, California
