
The swastika curve is the name given by Martyn Cundy and A. P. Rollett in their book Mathematical Models [1] to a type of quartic plane curve.

The swastika curve is the name given by Martyn Cundy and A. P. Rollett in their book Mathematical Models [1] to a type of quartic plane curve.
The plane curve with the Cartesian equation
or, equivalently, the polar equation
The curve looks similar to the right-handed swastika. It can be inverted with respect to a unit circle to resemble a left-handed swastika. The Cartesian equation then becomes a quartic curve,
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuthal angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system.
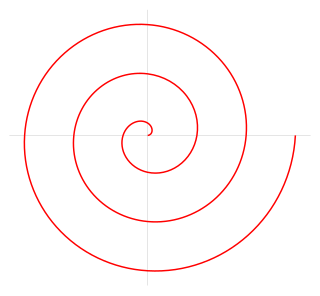
The Archimedean spiral is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
A nonholonomic system in physics and mathematics is a physical system whose state depends on the path taken in order to achieve it. Such a system is described by a set of parameters subject to differential constraints, such that when the system evolves along a path in its parameter space but finally returns to the original set of parameter values at the start of the path, the system itself may not have returned to its original state.

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization of the object.

In mathematics, a rose or rhodonea curve is a sinusoid specified by either the cosine or sine functions with no phase angle that is plotted in polar coordinates. Rose curves or "rhodonea" were named by the Italian mathematician who studied them, Guido Grandi, between the years 1723 and 1728.

In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the point on the circle opposite to the point of tangency. In fact, the curve family of cissoids is named for this example and some authors refer to it simply as the cissoid. It has a single cusp at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote. It is a member of the conchoid of de Sluze family of curves and in form it resembles a tractrix.
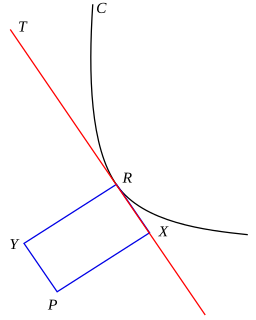
In mathematics, a pedal curve of a given curve results from the orthogonal projection of a fixed point on the tangent lines of this curve. More precisely, for a plane curve C and a given fixed pedal pointP, the pedal curve of C is the locus of points X so that the line PX is perpendicular to a tangent T to the curve passing through the point X. Conversely, at any point R on the curve C, let T be the tangent line at that point R; then there is a unique point X on the tangent T which forms with the pedal point P a line perpendicular to the tangent T – the pedal curve is the set of such points X, called the foot of the perpendicular to the tangent T from the fixed point P, as the variable point R ranges over the curve C.

In geometry, a cissoid is a curve generated from two given curves C1, C2 and a point O. Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2. Then the locus of such points P is defined to be the cissoid of the curves C1, C2 relative to O.

In geometry, the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve resembling the Greek letter ϰ (kappa). The kappa curve was first studied by Gérard van Gutschoven around 1662. In the history of mathematics, it is remembered as one of the first examples of Isaac Barrow's application of rudimentary calculus methods to determine the tangent of a curve. Isaac Newton and Johann Bernoulli continued the studies of this curve subsequently.
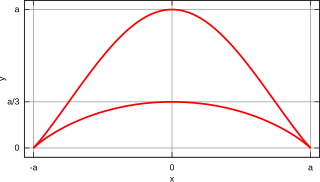
In geometry, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne, is a rational quartic curve defined by the equation

A cochleoid is a snail-shaped curve similar to a strophoid which can be represented by the polar equation
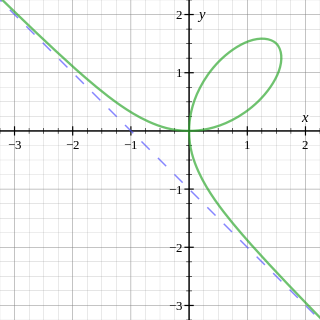
In geometry, the folium of Descartes is an algebraic curve defined by the equation

In geometry, a strophoid is a curve generated from a given curve C and points A and O as follows: Let L be a variable line passing through O and intersecting C at K. Now let P1 and P2 be the two points on L whose distance from K is the same as the distance from A to K. The locus of such points P1 and P2 is then the strophoid of C with respect to the pole O and fixed point A. Note that AP1 and AP2 are at right angles in this construction.
A quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.

In geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation

In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin.
For a plane curve C and a given fixed point O, the pedal equation of the curve is a relation between r and p where r is the distance from O to a point on C and p is the perpendicular distance from O to the tangent line to C at the point. The point O is called the pedal point and the values r and p are sometimes called the pedal coordinates of a point relative to the curve and the pedal point. It is also useful to measure the distance of O to the normal even though it is not an independent quantity and it relates to as .