 |
In the branch of mathematical logic known as type theory, System F<:, pronounced "F-sub", is an extension of system F with subtyping. System F<: has been of central importance to programming language theory since the 1980s[ citation needed ] because the core of functional programming languages, like those in the ML family, support both parametric polymorphism and record subtyping, which can be expressed in System F<:.
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning.
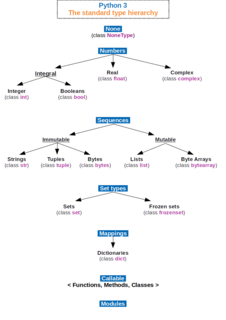
In computer science and computer programming, a data type is a set of possible values and a set of allowed operations on it. A data type tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans. A data type constrains the possible values that an expression, such as a variable or a function, might take. This data type defines the operations that can be done on the data, the meaning of the data, and the way values of that type can be stored.
In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a type to every "term". Usually the terms are various constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components.
In programming language theory, subtyping is a form of type polymorphism in which a subtype is a datatype that is related to another datatype by some notion of substitutability, meaning that program elements, typically subroutines or functions, written to operate on elements of the supertype can also operate on elements of the subtype. If S is a subtype of T, the subtyping relation means that any term of type S can safely be used in any context where a term of type T is expected. The precise semantics of subtyping here crucially depends on the particulars of how "safely be used" and "any context" are defined by a given type formalism or programming language. The type system of a programming language essentially defines its own subtyping relation, which may well be trivial, should the language support no conversion mechanisms.
In programming language theory and type theory, polymorphism is the provision of a single interface to entities of different types or the use of a single symbol to represent multiple different types. The concept is borrowed from a principle in biology where an organism or species can have many different forms or stages.
The Liskov substitution principle (LSP) is a particular definition of a subtyping relation, called strong behavioral subtyping, that was initially introduced by Barbara Liskov in a 1988 conference keynote address titled Data abstraction and hierarchy. It is based on the concept of "substitutability" – a principle in object-oriented programming stating that an object and a sub-object must be interchangeable without breaking the program. It is a semantic rather than merely syntactic relation, because it intends to guarantee semantic interoperability of types in a hierarchy, object types in particular. Barbara Liskov and Jeannette Wing described the principle succinctly in a 1994 paper as follows:
Subtype Requirement: Let be a property provable about objects of type T. Then should be true for objects of type S where S is a subtype of T.
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered. From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus, but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes.
System F is a typed lambda calculus that introduces, to simply typed lambda calculus, a mechanism of universal quantification over types. System F formalizes parametric polymorphism in programming languages, thus forming a theoretical basis for languages such as Haskell and ML. It was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds (1974).
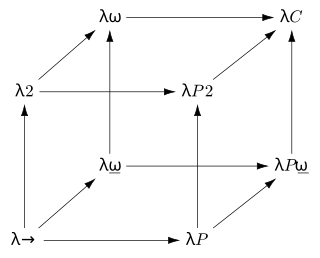
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
In computer science and logic, a dependent type is a type whose definition depends on a value. It is an overlapping feature of type theory and type systems. In intuitionistic type theory, dependent types are used to encode logic's quantifiers like "for all" and "there exists". In functional programming languages like Agda, ATS, Coq, F*, Epigram, and Idris, dependent types help reduce bugs by enabling the programmer to assign types that further restrain the set of possible implementations.
In programming languages and type theory, parametric polymorphism is a way to make a language more expressive, while still maintaining full static type-safety. Using parametric polymorphism, a function or a data type can be written generically so that it can handle values identically without depending on their type. Such functions and data types are called generic functions and generic datatypes respectively and form the basis of generic programming.
In type theory, a theory within mathematical logic, the bottom type is the type that has no values. It is also called the zero, never or empty type, and is sometimes denoted with the up tack (⊥) symbol.
In the study of formal theories in mathematical logic, bounded quantifiers are often included in a formal language in addition to the standard quantifiers "∀" and "∃". Bounded quantifiers differ from "∀" and "∃" in that bounded quantifiers restrict the range of the quantified variable. The study of bounded quantifiers is motivated by the fact that determining whether a sentence with only bounded quantifiers is true is often not as difficult as determining whether an arbitrary sentence is true.
In type theory, bounded quantification refers to universal or existential quantifiers which are restricted ("bounded") to range only over the subtypes of a particular type. Bounded quantification is an interaction of parametric polymorphism with subtyping. Bounded quantification has traditionally been studied in the functional setting of System F<:, but is available in modern object-oriented languages supporting parametric polymorphism (generics) such as Java, C# and Scala.
A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.
Gradual typing is a type system in which some variables and expressions may be given types and the correctness of the typing is checked at compile time and some expressions may be left untyped and eventual type errors are reported at runtime. Gradual typing allows software developers to choose either type paradigm as appropriate, from within a single language. In many cases gradual typing is added to an existing dynamic language, creating a derived language allowing but not requiring static typing to be used. In some cases a language uses gradual typing from the start.
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier in the first order formula expresses that everything in the domain satisfies the property denoted by . On the other hand, the existential quantifier in the formula expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable.
This programming language theory or type theory-related article is a stub. You can help Wikipedia by expanding it. |
