In calculus, the derivative of any linear combination of functions equals the same linear combination of the derivatives of the functions; this property is known as linearity of differentiation, the rule of linearity, or the superposition rule for differentiation. It is a fundamental property of the derivative that encapsulates in a single rule two simpler rules of differentiation, the sum rule and the constant factor rule. Thus it can be said that the act of differentiation is linear, or the differential operator is a linear operator.

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebras with additional structure. In general, a quantum group is some kind of Hopf algebra. There is no single, all-encompassing definition, but instead a family of broadly similar objects.
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.

In probability theory and statistics, the inverse gamma distribution is a two-parameter family of continuous probability distributions on the positive real line, which is the distribution of the reciprocal of a variable distributed according to the gamma distribution. Perhaps the chief use of the inverse gamma distribution is in Bayesian statistics, where the distribution arises as the marginal posterior distribution for the unknown variance of a normal distribution, if an uninformative prior is used, and as an analytically tractable conjugate prior, if an informative prior is required.
In differential geometry, a tensor density or relative tensor is a generalization of the tensor field concept. A tensor density transforms as a tensor field when passing from one coordinate system to another, except that it is additionally multiplied or weighted by a power W of the Jacobian determinant of the coordinate transition function or its absolute value. A distinction is made among (authentic) tensor densities, pseudotensor densities, even tensor densities and odd tensor densities. Sometimes tensor densities with a negative weight W are called tensor capacity. A tensor density can also be regarded as a section of the tensor product of a tensor bundle with a density bundle.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.

In mathematics, Eisenstein integers, occasionally also known as Eulerian integers, are complex numbers of the form
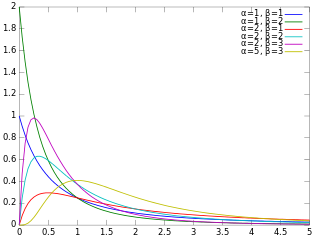
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution defined for with two parameters α and β, having the probability density function:
In mathematics, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
A quasiprobability distribution is a mathematical object similar to a probability distribution but which relaxes some of Kolmogorov's axioms of probability theory. Although quasiprobabilities share several of general features with ordinary probabilities, such as, crucially, the ability to yield expectation values with respect to the weights of the distribution, they all violate the σ-additivity axiom, because regions integrated under them do not represent probabilities of mutually exclusive states. To compensate, some quasiprobability distributions also counterintuitively have regions of negative probability density, contradicting the first axiom. Quasiprobability distributions arise naturally in the study of quantum mechanics when treated in phase space formulation, commonly used in quantum optics, time-frequency analysis, and elsewhere.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the space-time, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The most often-used variables in the formalism are the Weyl scalars, derived from the Weyl tensor. In particular, it can be shown that one of these scalars-- in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In mathematics, the hypergeometric function of a matrix argument is a generalization of the classical hypergeometric series. It is a function defined by an infinite summation which can be used to evaluate certain multivariate integrals.
In mathematics, the Jack function is a generalization of the Jack polynomial, introduced by Henry Jack. The Jack polynomial is a homogeneous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by the Heckman–Opdam polynomials and Macdonald polynomials.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to

The Flamant solution provides expressions for the stresses and displacements in a linear elastic wedge loaded by point forces at its sharp end. This solution was developed by A. Flamant in 1892 by modifying the three-dimensional solution of Boussinesq.
In set theory, a branch of mathematics, the Milner – Rado paradox, found by Eric Charles Milner and Richard Rado (1965), states that every ordinal number α less than the successor κ+ of some cardinal number κ can be written as the union of sets X1,X2,... where Xn is of order type at most κn for n a positive integer.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.
The table of chords, created by the astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Centuries passed before more extensive trigonometric tables were created. One such table is the Canon Sinuum created at the end of the 16th century.

The Mindlin–Reissner theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin. A similar, but not identical, theory had been proposed earlier by Eric Reissner in 1945. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Mindlin–Reissner theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of one tenth the planar dimensions while the Kirchhoff–Love theory is applicable to thinner plates.
Mustafa Tamer Başar, is a Turkish control theorist who holds the Swanlund Endowed Chair of the Center for Advanced Study and Professor in the Department of Electrical and Computer Engineering at the University of Illinois at Urbana-Champaign, USA.

In computing, a Digital Object Identifier orDOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.

The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.





























