In graph theory, the metric dimension of a graph G is the minimum cardinality of a subset S of vertices such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.

In graph theory, a dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is adjacent to at least one member of D. The domination number γ(G) is the number of vertices in a smallest dominating set for G.
In graph theory, a domatic partition of a graph is a partition of into disjoint sets , ,..., such that each Vi is a dominating set for G. The figure on the right shows a domatic partition of a graph; here the dominating set consists of the yellow vertices, consists of the green vertices, and consists of the blue vertices.
In graph theory, a connected dominating set and a maximum leaf spanning tree are two closely related structures defined on an undirected graph.
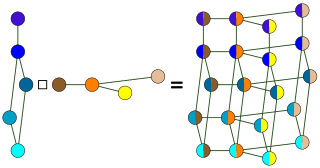
In graph theory, the Cartesian productGH of graphs G and H is a graph such that
In graph theory, Vizing's conjecture concerns a relation between the domination number and the cartesian product of graphs. This conjecture was first stated by Vadim G. Vizing (1968), and states that, if γ(G) denotes the minimum number of vertices in a dominating set for G, then

Martin Charles Golumbic is a mathematician and computer scientist, best known for his work in algorithmic graph theory and in artificial intelligence. He is the founding editor-in-chief of the journal Annals of Mathematics and Artificial Intelligence, published by Springer.
In mathematics, especially in the fields of universal algebra and graph theory, a graph algebra is a way of giving a directed graph an algebraic structure. It was introduced in, and has seen many uses in the field of universal algebra since then.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.

Gary Theodore Chartrand is an American-born mathematician who specializes in graph theory. He is known for his textbooks on introductory graph theory and for the concept of a highly irregular graph.
Renu Chakravarti Laskar is an Indian-born American mathematician, specializing in graph theory. She is Professor Emerita of Mathematical sciences at Clemson University. She received her Ph.D. in Mathematics from the University of Illinois at Urbana-Champaign in 1962.
Michael S. Jacobson is a mathematician, and Professor of Mathematical & Statistical Sciences in the Department of Mathematical & Statistical Science at the University of Colorado Denver. He served as Chair from 2003 to 2012 and was on loan serving as a program director in EHR/DUE at the National Science Foundation.
Richard F. Johnsonbaugh is an American mathematician and computer scientist. His interests include discrete mathematics and the history of mathematics. He is the author of several textbooks.
Claudio Procesi is an Italian mathematician, known for works in algebra and representation theory.
Phyllis Zweig Chinn is an American mathematician who holds a professorship in mathematics, women's studies, and teaching preparation at Humboldt State University in California. Her publications concern graph theory, mathematics education, and the history of women in mathematics.
In graph theory, an eternal dominating set for a graph G = (V, E) is a subset D of V such that D is a dominating set on which mobile guards are initially located. The set D must be such that for any infinite sequence of attacks occurring sequentially at vertices, the set D can be modified by moving a guard from an adjacent vertex to the attacked vertex, provided the attacked vertex has no guard on it at the time it is attacked. The configuration of guards after each attack must induce a dominating set. The eternal domination number, γ∞(G), is the minimum number of vertices possible in the initial set D. For example, the eternal domination number of the cycle on five vertices is two.
Ortrud R. Oellermann is a South African mathematician specializing in graph theory. She is a professor of mathematics at the University of Winnipeg.
Christina Magdalena (Kieka) Mynhardt is a South African mathematician known for her work on dominating sets in graph theory, including domination versions of the eight queens puzzle. She is a professor of mathematics and statistics at the University of Victoria in Canada.
Odile Zink-Favaron is a French mathematician known for her research in graph theory, including work on well-covered graphs, factor-critical graphs, spectral graph theory, Hamiltonian decomposition, and dominating sets. She is retired from the Laboratory for Computer Science (LRI) at the University of Paris-Sud.
Mirka Miller was a Czech-Australian mathematician and computer scientist interested in graph theory and data security. She was a professor of electrical engineering and computer science at the University of Newcastle.





