
In number theory, a Carmichael number is a composite number which in modular arithmetic satisfies the congruence relation:
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers A with positive natural density contains a k-term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.
In number theory, the Elliott–Halberstam conjecture is a conjecture about the distribution of prime numbers in arithmetic progressions. It has many applications in sieve theory. It is named for Peter D. T. A. Elliott and Heini Halberstam, who stated the conjecture in 1968.

Ben Joseph Green FRS is a British mathematician, specialising in combinatorics and number theory. He is the Waynflete Professor of Pure Mathematics at the University of Oxford.
In combinatorial number theory, the Erdős–Graham problem is the problem of proving that, if the set of integers greater than one is partitioned into finitely many subsets, then one of the subsets can be used to form an Egyptian fraction representation of unity. That is, for every , and every -coloring of the integers greater than one, there is a finite monochromatic subset of these integers such that
Erdős' conjecture on arithmetic progressions, often referred to as the Erdős–Turán conjecture, is a conjecture in arithmetic combinatorics. It states that if the sum of the reciprocals of the members of a set A of positive integers diverges, then A contains arbitrarily long arithmetic progressions.
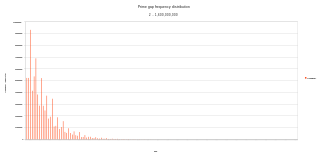
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.
In number theory, the Green–Tao theorem, proved by Ben Green and Terence Tao in 2004, states that the sequence of prime numbers contains arbitrarily long arithmetic progressions. In other words, for every natural number k, there exist arithmetic progressions of primes with k terms. The proof is an extension of Szemerédi's theorem. The problem can be traced back to investigations of Lagrange and Waring from around 1770.
In additive combinatorics and number theory, a subset A of an abelian group G is said to be sum-free if the sumset A + A is disjoint from A. In other words, A is sum-free if the equation has no solution with .
In mathematics, arithmetic combinatorics is a field in the intersection of number theory, combinatorics, ergodic theory and harmonic analysis.
In number theory, a Sidon sequence is a sequence of natural numbers in which all pairwise sums (for ) are different. Sidon sequences are also called Sidon sets; they are named after the Hungarian mathematician Simon Sidon, who introduced the concept in his investigations of Fourier series.
In arithmetic combinatorics, the Erdős–Szemerédi theorem states that for every finite set of integers, at least one of , the set of pairwise sums or , the set of pairwise products form a significantly larger set. More precisely, the Erdős–Szemerédi theorem states that there exist positive constants c and such that for any non-empty set
Tom Sanders is an English mathematician, working on problems in additive combinatorics at the interface of harmonic analysis and analytic number theory.

James Alexander Maynard is an English mathematician working in analytic number theory and in particular the theory of prime numbers. In 2017, he was appointed Research Professor at Oxford. Maynard is a fellow of St John's College, Oxford. He was awarded the Fields Medal in 2022 and the New Horizons in Mathematics Prize in 2023.
In mathematics, a square-difference-free set is a set of natural numbers, no two of which differ by a square number. Hillel Furstenberg and András Sárközy proved in the late 1970s the Furstenberg–Sárközy theorem of additive number theory showing that, in a certain sense, these sets cannot be very large. In the game of subtract a square, the positions where the next player loses form a square-difference-free set. Another square-difference-free set is obtained by doubling the Moser–de Bruijn sequence.

In mathematics, and in particular in arithmetic combinatorics, a Salem-Spencer set is a set of numbers no three of which form an arithmetic progression. Salem–Spencer sets are also called 3-AP-free sequences or progression-free sets. They have also been called non-averaging sets, but this term has also been used to denote a set of integers none of which can be obtained as the average of any subset of the other numbers. Salem-Spencer sets are named after Raphaël Salem and Donald C. Spencer, who showed in 1942 that Salem–Spencer sets can have nearly-linear size. However a later theorem of Klaus Roth shows that the size is always less than linear.
Roth's theorem on arithmetic progressions is a result in additive combinatorics concerning the existence of arithmetic progressions in subsets of the natural numbers. It was first proven by Klaus Roth in 1953. Roth's theorem is a special case of Szemerédi's theorem for the case .
Daniel Larsen is an American mathematician known for proving a 1994 conjecture of W. R. Alford, Andrew Granville and Carl Pomerance on the distribution of Carmichael numbers, commonly known as Bertrand's postulate for Carmichael numbers.











