Financial economics is the branch of economics characterized by a "concentration on monetary activities", in which "money of one type or another is likely to appear on both sides of a trade". Its concern is thus the interrelation of financial variables, such as share prices, interest rates and exchange rates, as opposed to those concerning the real economy. It has two main areas of focus: asset pricing and corporate finance; the first being the perspective of providers of capital, i.e. investors, and the second of users of capital. It thus provides the theoretical underpinning for much of finance.
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments, using various underlying assumptions. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.
In financial mathematics, the implied volatility (IV) of an option contract is that value of the volatility of the underlying instrument which, when input in an option pricing model, will return a theoretical value equal to the price of said option. A non-option financial instrument that has embedded optionality, such as an interest rate cap, can also have an implied volatility. Implied volatility, a forward-looking and subjective measure, differs from historical volatility because the latter is calculated from known past returns of a security. To understand where implied volatility stands in terms of the underlying, implied volatility rank is used to understand its implied volatility from a one-year high and low IV.
In finance, moneyness is the relative position of the current price of an underlying asset with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification:

Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money.
A variance swap is an over-the-counter financial derivative that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock index.
In mathematical finance, the Black–Derman–Toy model (BDT) is a popular short-rate model used in the pricing of bond options, swaptions and other interest rate derivatives; see Lattice model (finance) § Interest rate derivatives. It is a one-factor model; that is, a single stochastic factor—the short rate—determines the future evolution of all interest rates. It was the first model to combine the mean-reverting behaviour of the short rate with the log-normal distribution, and is still widely used.
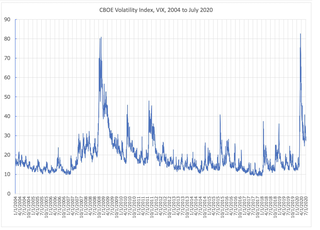
VIX is the ticker symbol and the popular name for the Chicago Board Options Exchange's CBOE Volatility Index, a popular measure of the stock market's expectation of volatility based on S&P 500 index options. It is calculated and disseminated on a real-time basis by the CBOE, and is often referred to as the fear index or fear gauge.
In finance, a price (premium) is paid or received for purchasing or selling options. This article discusses the calculation of this premium in general. For further detail, see: Mathematical finance § Derivatives pricing: the Q world for discussion of the mathematics; Financial engineering for the implementation; as well as Financial modeling § Quantitative finance generally.
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others.
The following outline is provided as an overview of and topical guide to finance:
In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.
In finance, an option is a contract which conveys to its owner, the holder, the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in over-the-counter (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts.
In finance, a volatility swap is a forward contract on the future realised volatility of a given underlying asset. Volatility swaps allow investors to trade the volatility of an asset directly, much as they would trade a price index. Its payoff at expiration is equal to
In finance, the Heston model, named after Steven L. Heston, is a mathematical model that describes the evolution of the volatility of an underlying asset. It is a stochastic volatility model: such a model assumes that the volatility of the asset is not constant, nor even deterministic, but follows a random process.
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats volatility as a function of both the current asset level and of time . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant. Local volatility models are often compared with stochastic volatility models, where the instantaneous volatility is not just a function of the asset level but depends also on a new "global" randomness coming from an additional random component.

In finance, volatility is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns.
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling of financial markets.
The Bachelier model is a model of an asset price under Brownian motion presented by Louis Bachelier on his PhD thesis The Theory of Speculation. It is also called "Normal Model" equivalently.
An additive process, in probability theory, is a cadlag, continuous in probability stochastic process with independent increments. An additive process is the generalization of a Lévy process. An example of an additive process that is not a Lévy process is a Brownian motion with a time-dependent drift. The additive process was introduced by Paul Lévy in 1937.


