In linear algebra, the determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix. The determinant of a matrix A is denoted det(A), det A, or |A|. Geometrically, it can be viewed as the volume scaling factor of the linear transformation described by the matrix. This is also the signed volume of the n-dimensional parallelepiped spanned by the column or row vectors of the matrix. The determinant is positive or negative according to whether the linear mapping preserves or reverses the orientation of n-space.

In mathematics, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The result matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix.
In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant. For instance, the following matrix is a Toeplitz matrix:

In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation.
In linear algebra, an n-by-n square matrix A is called invertible if there exists an n-by-n square matrix B such that
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix as coefficients. The characteristic polynomial of an endomorphism of vector spaces of finite dimension is the characteristic polynomial of the matrix of the endomorphism over any base; it does not depend on the choice of a basis. The characteristic equation is the equation obtained by equating to zero the characteristic polynomial.

In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra. In common geometrical contexts, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction. The term "scalar" itself derives from this usage: a scalar is that which scales vectors. Scalar multiplication is the multiplication of a vector by a scalar, and must be distinguished from inner product of two vectors.
In mathematics, and in particular linear algebra, the Moore–Penrose inverse of a matrix is the most widely known generalization of the inverse matrix. It was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951, and Roger Penrose in 1955. Earlier, Erik Ivar Fredholm had introduced the concept of a pseudoinverse of integral operators in 1903. When referring to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose inverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse.
In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned.
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal only.
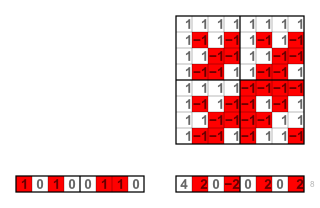
The Hadamard transform is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on 2m real numbers.

In classical cryptography, the Hill cipher is a polygraphic substitution cipher based on linear algebra. Invented by Lester S. Hill in 1929, it was the first polygraphic cipher in which it was practical to operate on more than three symbols at once. The following discussion assumes an elementary knowledge of matrices.
In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain (PID). The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices. In particular, the integers are a PID, so one can always calculate the Smith normal form of an integer matrix. The Smith normal form is very useful for working with finitely generated modules over a PID, and in particular for deducing the structure of a quotient of a free module. It is named after the British mathematician Henry John Stephen Smith.
In mathematics, in the area of wavelet analysis, a refinable function is a function which fulfils some kind of self-similarity. A function is called refinable with respect to the mask if
In applied mathematics, the transfer matrix is a formulation in terms of a block-Toeplitz matrix of the two-scale equation, which characterizes refinable functions. Refinable functions play an important role in wavelet theory and finite element theory.
Fugue is a cryptographic hash function submitted by IBM to the NIST hash function competition. It was designed by Shai Halevi, William E. Hall, and Charanjit S. Jutla. Fugue takes an arbitrary-length message and compresses it down to a fixed bit-length. The hash functions for the different output lengths are called Fugue-224, Fugue-256, Fugue-384 and Fugue-512. The authors also describe a parametrized version of Fugue. A weak version of Fugue-256 is also described using this parameterized version.
In discrete mathematics, ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as ideal lattices. They can be used in cryptosystems to decrease by a square root the number of parameters necessary to describe a lattice, making them more efficient. Ideal lattices are a new concept, but similar lattice classes have been used for a long time. For example cyclic lattices, a special case of ideal lattices, are used in NTRUEncrypt and NTRUSign.
Rendezvous or highest random weight (HRW) hashing is an algorithm that allows clients to achieve distributed agreement on a set of options out of a possible set of options. A typical application is when clients need to agree on which sites objects are assigned to.
In mathematics, the Zassenhaus algorithm is a method to calculate a basis for the intersection and sum of two subspaces of a vector space. It is named after Hans Zassenhaus, but no publication of this algorithm by him is known. It is used in computer algebra systems.








