Top-down parsing

Last updated

Top-down parsing in computer science is a parsing strategy where one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar. [1] LL parsers are a type of parser that uses a top-down parsing strategy.

Contents

Top-down parsing is a strategy of analyzing unknown data relationships by hypothesizing general parse tree structures and then considering whether the known fundamental structures are compatible with the hypothesis. It occurs in the analysis of both natural languages and computer languages.

Top-down parsing can be viewed as an attempt to find left-most derivations of an input-stream by searching for parse-trees using a top-down expansion of the given formal grammar rules. Inclusive choice is used to accommodate ambiguity by expanding all alternative right-hand-sides of grammar rules. [2]

Simple implementations of top-down parsing do not terminate for left-recursive grammars, and top-down parsing with backtracking may have exponential time complexity with respect to the length of the input for ambiguous CFGs. [3] However, more sophisticated top-down parsers have been created by Frost, Hafiz, and Callaghan, [4] [5] which do accommodate ambiguity and left recursion in polynomial time and which generate polynomial-sized representations of the potentially exponential number of parse trees.

Programming language application

A compiler parses input from a programming language to an internal representation by matching the incoming symbols to production rules. Production rules are commonly defined using Backus–Naur form. An LL parser is a type of parser that does top-down parsing by applying each production rule to the incoming symbols, working from the left-most symbol yielded on a production rule and then proceeding to the next production rule for each non-terminal symbol encountered. In this way the parsing starts on the Left of the result side (right side) of the production rule and evaluates non-terminals from the Left first and, thus, proceeds down the parse tree for each new non-terminal before continuing to the next symbol for a production rule.

For example:

which produces the string A=acdf

would match and attempt to match next. Then would be tried. As one may expect, some languages are more ambiguous than others. For a non-ambiguous language, in which all productions for a non-terminal produce distinct strings, the string produced by one production will not start with the same symbol as the string produced by another production. A non-ambiguous language may be parsed by an LL(1) grammar where the (1) signifies the parser reads ahead one token at a time. For an ambiguous language to be parsed by an LL parser, the parser must lookahead more than 1 symbol, e.g. LL(3).

The common solution to this problem is to use an LR parser, which is a type of shift-reduce parser, and does bottom-up parsing.

Accommodating left recursion in top-down parsing

A formal grammar that contains left recursion cannot be parsed by a naive recursive descent parser unless they are converted to a weakly equivalent right-recursive form. However, recent research demonstrates that it is possible to accommodate left-recursive grammars (along with all other forms of general CFGs) in a more sophisticated top-down parser by use of curtailment. A recognition algorithm that accommodates ambiguous grammars and curtails an ever-growing direct left-recursive parse by imposing depth restrictions with respect to input length and current input position, is described by Frost and Hafiz in 2006. [6] That algorithm was extended to a complete parsing algorithm to accommodate indirect (by comparing previously computed context with current context) as well as direct left-recursion in polynomial time, and to generate compact polynomial-size representations of the potentially exponential number of parse trees for highly ambiguous grammars by Frost, Hafiz and Callaghan in 2007. [4] The algorithm has since been implemented as a set of parser combinators written in the Haskell programming language. The implementation details of these new set of combinators can be found in a paper [5] by the authors, which was presented in PADL'08. The X-SAIGA site has more about the algorithms and implementation details.

Additionally, one may use a Graph-structured stack (GSS) in addition to the aforementioned curtailment in order to accommodate left recursion by 'merging' stacks with common prefixes and by preventing infinite recursion, thereby reducing the number and contents of each stack, thereby reducing the time and space complexity of the parser. This leads to a algorithm known as Generalized LL parsing, in which you use a GSS, left-recursion curtailment, and an LL(k) parser to parse input strings relative to a given CFG. [7] [8]

Time and space complexity of top-down parsing

When top-down parser tries to parse an ambiguous input with respect to an ambiguous CFG, it may need exponential number of steps (with respect to the length of the input) to try all alternatives of the CFG in order to produce all possible parse trees, which eventually would require exponential memory space. The problem of exponential time complexity in top-down parsers constructed as sets of mutually recursive functions has been solved by Norvig in 1991. [9] His technique is similar to the use of dynamic programming and state-sets in Earley's algorithm (1970), and tables in the CYK algorithm of Cocke, Younger and Kasami.

The key idea is to store results of applying a parser p at position j in a memorable and to reuse results whenever the same situation arises. Frost, Hafiz and Callaghan [4] [5] also use memoization for refraining redundant computations to accommodate any form of CFG in polynomial time (Θ(n4) for left-recursive grammars and Θ(n3) for non left-recursive grammars). Their top-down parsing algorithm also requires polynomial space for potentially exponential ambiguous parse trees by 'compact representation' and 'local ambiguities grouping'. Their compact representation is comparable with Tomita's compact representation of bottom-up parsing. [10]

Using PEG's, another representation of grammars, packrat parsers provide an elegant and powerful parsing algorithm. See Parsing expression grammar.

Examples

Some of the parsers that use top-down parsing include:

See also

Related Research Articles

In formal language theory, computer science and linguistics, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars. This hierarchy of grammars was described by Noam Chomsky in 1956.

<span class="mw-page-title-main">Context-free grammar</span> Type of formal grammar

In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form

In computer science, the Earley parser is an algorithm for parsing strings that belong to a given context-free language, though it may suffer problems with certain nullable grammars. The algorithm, named after its inventor, Jay Earley, is a chart parser that uses dynamic programming; it is mainly used for parsing in computational linguistics. It was first introduced in his dissertation in 1968.

In computer science, LR parsers are a type of bottom-up parser that analyse deterministic context-free languages in linear time. There are several variants of LR parsers: SLR parsers, LALR parsers, Canonical LR(1) parsers, Minimal LR(1) parsers, and GLR parsers. LR parsers can be generated by a parser generator from a formal grammar defining the syntax of the language to be parsed. They are widely used for the processing of computer languages.

<span class="mw-page-title-main">L-system</span> Rewriting system and type of formal grammar

An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems were introduced and developed in 1968 by Aristid Lindenmayer, a Hungarian theoretical biologist and botanist at the University of Utrecht. Lindenmayer used L-systems to describe the behaviour of plant cells and to model the growth processes of plant development. L-systems have also been used to model the morphology of a variety of organisms and can be used to generate self-similar fractals.

In computer science, the Cocke–Younger–Kasami algorithm is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming.

In computer science, an LL parser is a top-down parser for a restricted context-free language. It parses the input from Left to right, performing Leftmost derivation of the sentence.

In computer science, a recursive descent parser is a kind of top-down parser built from a set of mutually recursive procedures where each such procedure implements one of the nonterminals of the grammar. Thus the structure of the resulting program closely mirrors that of the grammar it recognizes.

Grammar theory to model symbol strings originated from work in computational linguistics aiming to understand the structure of natural languages. Probabilistic context free grammars (PCFGs) have been applied in probabilistic modeling of RNA structures almost 40 years after they were introduced in computational linguistics.

Parsing, syntax analysis, or syntactic analysis is the process of analyzing a string of symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar. The term parsing comes from Latin pars (orationis), meaning part.

In computing, memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. Memoization has also been used in other contexts, such as in simple mutually recursive descent parsing. Although related to caching, memoization refers to a specific case of this optimization, distinguishing it from forms of caching such as buffering or page replacement. In the context of some logic programming languages, memoization is also known as tabling.

In computer science, a parsing expression grammar (PEG) is a type of analytic formal grammar, i.e. it describes a formal language in terms of a set of rules for recognizing strings in the language. The formalism was introduced by Bryan Ford in 2004 and is closely related to the family of top-down parsing languages introduced in the early 1970s. Syntactically, PEGs also look similar to context-free grammars (CFGs), but they have a different interpretation: the choice operator selects the first match in PEG, while it is ambiguous in CFG. This is closer to how string recognition tends to be done in practice, e.g. by a recursive descent parser.

In the formal language theory of computer science, left recursion is a special case of recursion where a string is recognized as part of a language by the fact that it decomposes into a string from that same language and a suffix. For instance, can be recognized as a sum because it can be broken into , also a sum, and , a suitable suffix.

ID/LP Grammars are a subset of Phrase Structure Grammars, differentiated from other formal grammars by distinguishing between immediate dominance (ID) and linear precedence (LP) constraints. Whereas traditional phrase structure rules incorporate dominance and precedence into a single rule, ID/LP Grammars maintains separate rule sets which need not be processed simultaneously. ID/LP Grammars are used in Computational Linguistics.

In computer science, a grammar is informally called a recursive grammar if it contains production rules that are recursive, meaning that expanding a non-terminal according to these rules can eventually lead to a string that includes the same non-terminal again. Otherwise it is called a non-recursive grammar.

In computer programming, a parser combinator is a higher-order function that accepts several parsers as input and returns a new parser as its output. In this context, a parser is a function accepting strings as input and returning some structure as output, typically a parse tree or a set of indices representing locations in the string where parsing stopped successfully. Parser combinators enable a recursive descent parsing strategy that facilitates modular piecewise construction and testing. This parsing technique is called combinatory parsing.

In formal language theory, a grammar describes how to form strings from a language's alphabet that are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language.

A filtered-popping recursive transition network (FPRTN), or simply filtered-popping network (FPN), is a recursive transition network (RTN) extended with a map of states to keys where returning from a subroutine jump requires the acceptor and return states to be mapped to the same key. RTNs are finite-state machines that can be seen as finite-state automata extended with a stack of return states; as well as consuming transitions and -transitions, RTNs may define call transitions. These transitions perform a subroutine jump by pushing the transition's target state onto the stack and bringing the machine to the called state. Each time an acceptor state is reached, the return state at the top of the stack is popped out, provided that the stack is not empty, and the machine is brought to this state.

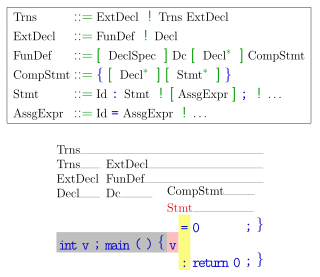
<span class="mw-page-title-main">LL grammar</span> Type of a context-free grammar

In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.

PackCC is a parser generator for C. Its main features are as follows:

References

  1. ↑ Dick Grune; Ceriel J.H. Jacobs (29 October 2007). Parsing Techniques: A Practical Guide. Springer Science & Business Media. ISBN   978-0-387-68954-8.
  2. ↑ Aho, Alfred V.; Sethi, Ravi; Ullman, Jeffrey D. (1986). Compilers, principles, techniques, and tools (Rep. with corrections. ed.). Addison-Wesley Pub. Co. ISBN   978-0201100884.
  3. ↑ Aho, Alfred V.; Ullman, Jeffrey D. (1972). The Theory of Parsing, Translation, and Compiling (Volume 1: Parsing.) (Repr. ed.). Englewood Cliffs, NJ: Prentice-Hall. ISBN   978-0139145568.
  4. 1 2 3 Frost, R., Hafiz, R. and Callaghan, P. (2007) " Modular and Efficient Top-Down Parsing for Ambiguous Left-Recursive Grammars ." 10th International Workshop on Parsing Technologies (IWPT), ACL-SIGPARSE , Pages: 109 - 120, June 2007, Prague. Archived from the original on 12 November 2018.
  5. 1 2 3 Frost, R., Hafiz, R. and Callaghan, P. (2008) " Parser Combinators for Ambiguous Left-Recursive Grammars." 10th International Symposium on Practical Aspects of Declarative Languages (PADL), ACM-SIGPLAN , Volume 4902/2008, Pages: 167-181, January 2008, San Francisco.
  6. ↑ Frost, R. and Hafiz, R. (2006) " A New Top-Down Parsing Algorithm to Accommodate Ambiguity and Left Recursion in Polynomial Time." ACM SIGPLAN Notices, Volume 41 Issue 5, Pages: 46 - 54. doi : 10.1145/1149982.1149988
  7. ↑ http://dotat.at/tmp/gll.pdf [ bare URL PDF ]
  8. ↑ https://pure.royalholloway.ac.uk/portal/files/26408385/postprint.pdf [ bare URL PDF ]
  9. ↑ Norvig, P. (1991) “Techniques for automatic memoisation with applications to context-free parsing.” Journal - Computational Linguistics Volume 17, Issue 1, Pages: 91 - 98.
  10. ↑ Tomita, M. (1985) “Efficient Parsing for Natural Language.” Kluwer, Boston, MA.
  11. ↑ Pereira, Fernando CN, and David HD Warren. "Definite clause grammars for language analysis—a survey of the formalism and a comparison with augmented transition networks." Artificial intelligence 13.3 (1980): 231-278.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.