
Half-life is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive. The term is also used more generally to characterize any type of exponential decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life is doubling time.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.
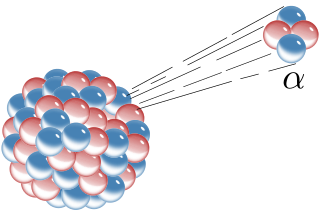
Radioactive decay is the process by which an unstable atomic nucleus loses energy by radiation. A material containing unstable nuclei is considered radioactive. Three of the most common types of decay are alpha, beta, and gamma decay. The weak force is the mechanism that is responsible for beta decay, while the other two are governed by the electromagnetism and nuclear force.

In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.

A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and λ (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant:
The Lotka–Volterra equations, also known as the Lotka–Volterra predator–prey model, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.

In the context of radioactivity, activity or total activity (symbol A) is a physical quantity defined as the number of radioactive transformations per second that occur in a particular radionuclide. The unit of activity is the becquerel (symbol Bq), which is defined equivalent to reciprocal seconds (symbol s-1). The older, non-SI unit of activity is the curie (Ci), which is 3.7×1010 radioactive decay per second. Another unit of activity is the rutherford, which is defined as 1×106 radioactive decay per second.
In physics, the Saha ionization equation is an expression that relates the ionization state of a gas in thermal equilibrium to the temperature and pressure. The equation is a result of combining ideas of quantum mechanics and statistical mechanics and is used to explain the spectral classification of stars. The expression was developed by physicist Meghnad Saha in 1920.
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include viscous damping in a fluid, surface friction, radiation, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes. Damping is not to be confused with friction, which is a type of dissipative force acting on a system. Friction can cause or be a factor of damping.
In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium. Each relaxation process can be categorized by a relaxation time τ. The simplest theoretical description of relaxation as function of time t is an exponential law exp(−t/τ).
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
The birth–death process is a special case of continuous-time Markov process where the state transitions are of only two types: "births", which increase the state variable by one and "deaths", which decrease the state by one. It was introduced by William Feller. The model's name comes from a common application, the use of such models to represent the current size of a population where the transitions are literal births and deaths. Birth–death processes have many applications in demography, queueing theory, performance engineering, epidemiology, biology and other areas. They may be used, for example, to study the evolution of bacteria, the number of people with a disease within a population, or the number of customers in line at the supermarket.

In electrochemistry, and more generally in solution chemistry, a Pourbaix diagram, also known as a potential/pH diagram, EH–pH diagram or a pE/pH diagram, is a plot of possible thermodynamically stable phases of an aqueous electrochemical system. Boundaries (50 %/50 %) between the predominant chemical species are represented by lines. As such a Pourbaix diagram can be read much like a standard phase diagram with a different set of axes. Similarly to phase diagrams, they do not allow for reaction rate or kinetic effects. Beside potential and pH, the equilibrium concentrations are also dependent upon, e.g., temperature, pressure, and concentration. Pourbaix diagrams are commonly given at room temperature, atmospheric pressure, and molar concentrations of 10−6 and changing any of these parameters will yield a different diagram.
In nuclear physics, secular equilibrium is a situation in which the quantity of a radioactive isotope remains constant because its production rate is equal to its decay rate.
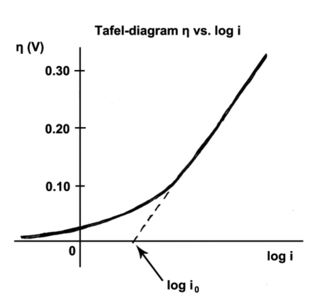
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential. The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.
" It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction ".

In nuclear physics, the Bateman equation is a mathematical model describing abundances and activities in a decay chain as a function of time, based on the decay rates and initial abundances. The model was formulated by Ernest Rutherford in 1905 and the analytical solution was provided by Harry Bateman in 1910.
Potassium–calcium dating, abbreviated K–Ca dating, is a radiometric dating method used in geochronology. It is based upon measuring the ratio of a parent isotope of potassium to a daughter isotope of calcium. This form of radioactive decay is accomplished through beta decay.
In mathematics, Liouville–Bratu–Gelfand equation or Liouville's equation is a non-linear Poisson equation, named after the mathematicians Joseph Liouville, Gheorghe Bratu and Israel Gelfand. The equation reads


















