Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics, therefore, excludes topics in "continuous mathematics" such as calculus and analysis.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
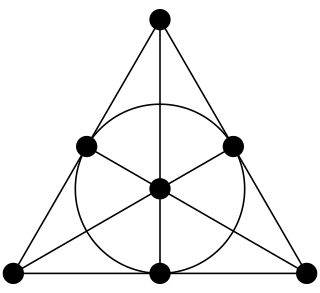
In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here, PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.
In mathematics, a combinatorial class is a countable set of mathematical objects, together with a size function mapping each object to a non-negative integer, such that there are finitely many objects of each size.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence, construction and properties of systems of finite sets whose arrangements satisfy generalized concepts of balance and/or symmetry. These concepts are not made precise so that a wide range of objects can be thought of as being under the same umbrella. At times this might involve the numerical sizes of set intersections as in block designs, while at other times it could involve the spatial arrangement of entries in an array as in sudoku grids.
Lottery mathematics is used to calculate probabilities of winning or losing a lottery game. It is based primarily on combinatorics, particularly the twelvefold way and combinations without replacement.

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

The Colorado Lottery is run by the state government of Colorado. It is a member of the Multi-State Lottery Association(MUSL).

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.

In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the plane trees with a given set of leaves, the ways of inserting parentheses into a sequence, and the ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin
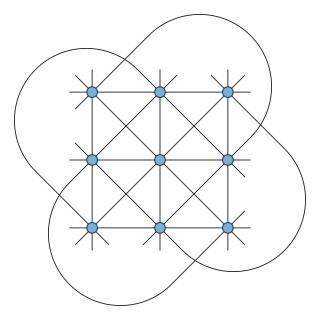
In geometry, the Hesse configuration is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane. It was introduced by Colin Maclaurin and studied by Hesse, and is also known as Young's geometry, named after the later work of John Wesley Young on finite geometry.
Rota's excluded minors conjecture is one of a number of conjectures made by the mathematician Gian-Carlo Rota. It is considered an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture was announced, but not published, in 2014 by Geelen, Gerards, and Whittle.
In discrete and computational geometry, a set of points in the Euclidean plane or a higher-dimensional Euclidean space is said to be in convex position or convex independent if none of the points can be represented as a convex combination of the others. A finite set of points is in convex position if all of the points are vertices of their convex hull. More generally, a family of convex sets is said to be in convex position if they are pairwise disjoint and none of them is contained in the convex hull of the others.











