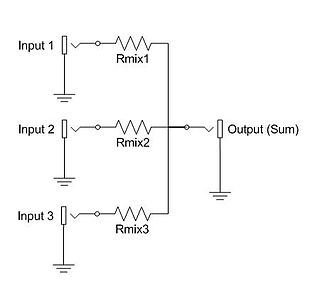
An electronic mixer is a device that combines two or more electrical or electronic signals into one or two composite output signals. There are two basic circuits that both use the term mixer, but they are very different types of circuits: additive mixers and multiplicative mixers. Additive mixers are also known as analog adders to distinguish from the related digital adder circuits.
In poetry, metre or meter is the basic rhythmic structure of a verse or lines in verse. Many traditional verse forms prescribe a specific verse metre, or a certain set of metres alternating in a particular order. The study and the actual use of metres and forms of versification are both known as prosody.

In physics, the Navier–Stokes equations are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
The molar gas constant is denoted by the symbol R or R. It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per mole, i.e. the pressure–volume product, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.
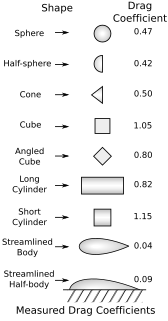
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area.
In mathematics, the indefinite orthogonal group, O(p, q) is the Lie group of all linear transformations of an n-dimensional real vector space that leave invariant a nondegenerate, symmetric bilinear form of signature (p, q), where n = p + q. It is also called the pseudo-orthogonal group or generalized orthogonal group. The dimension of the group is n(n − 1)/2.
In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin-Louis Cauchy.
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform.
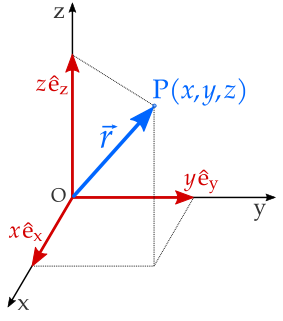
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents the position of a point P in space in relation to an arbitrary reference origin O. Usually denoted x, r, or s, it corresponds to the straight line segment from O to P. In other words, it is the displacement or translation that maps the origin to P:

In system analysis, among other fields of study, a linear time-invariant system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined below. These properties apply to many important physical systems, in which case the response y(t) of the system to an arbitrary input x(t) can be found directly using convolution: y(t) = x(t) ∗ h(t) where h(t) is called the system's impulse response and ∗ represents convolution. What's more, there are systematic methods for solving any such system, whereas systems not meeting both properties are generally more difficult to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers.

In combinatorics, the rule of product or multiplication principle is a basic counting principle. Stated simply, it is the intuitive idea that if there are a ways of doing something and b ways of doing another thing, then there are a · b ways of performing both actions.
Friis formula or Friis's formula, named after Danish-American electrical engineer Harald T. Friis, is either of two formulas used in telecommunications engineering to calculate the signal-to-noise ratio of a multistage amplifier. One relates to noise factor while the other relates to noise temperature.

An electrochemical gradient is a gradient of electrochemical potential, usually for an ion that can move across a membrane. The gradient consists of two parts, the chemical gradient, or difference in solute concentration across a membrane, and the electrical gradient, or difference in charge across a membrane. When there are unequal concentrations of an ion across a permeable membrane, the ion will move across the membrane from the area of higher concentration to the area of lower concentration through simple diffusion. Ions also carry an electric charge that forms an electric potential across a membrane. If there is an unequal distribution of charges across the membrane, then the difference in electric potential generates a force that drives ion diffusion until the charges are balanced on both sides of the membrane.

Reverend Ferdinand Kittel was a Lutheran priest and indologist with the Basel Mission in south India and worked in Mangalore, Madikeri and Dharwad in Karnataka. He is most famous for his studies of the Kannada language and for producing a Kannada-English dictionary of about 70,000 words in 1894. He also composed numerous Kannada poems.
The relative velocity is the velocity of an object or observer B in the rest frame of another object or observer A.
Covariance matrix adaptation evolution strategy (CMA-ES) is a particular kind of strategy for numerical optimization. Evolution strategies (ES) are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation. An evolutionary algorithm is broadly based on the principle of biological evolution, namely the repeated interplay of variation and selection: in each generation (iteration) new individuals are generated by variation, usually in a stochastic way, of the current parental individuals. Then, some individuals are selected to become the parents in the next generation based on their fitness or objective function value . Like this, over the generation sequence, individuals with better and better -values are generated.
Kannada prosody is the study of metres used in Kannada poetry, describing the rhythmic structure of a verse. The metres used include some metres borrowed from other traditions, and indigenous metres. Kannada literature, especially Old Kannada poetry, clearly exhibits the importance poets placed on metre. This can be seen in the number of types of metre used in Kannada poetry.
The Vanna–Volga method is a mathematical tool used in finance. It is a technique for pricing first-generation exotic options in foreign exchange market (FX) derivatives.
In Mathematics, the Lindström–Gessel–Viennot lemma provides a way to count the number of tuples of non-intersecting lattice paths, or, more generally, paths on a directed graph. It was proved by Gessel–Viennot in 1985, based on previous work of Lindström published in 1973.
In mathematics, more specifically, in convex geometry, the mixed volume is a way to associate a non-negative number to an -tuple of convex bodies in -dimensional space. This number depends on the size and shape of the bodies and on their relative orientation to each other.
















