Related Research Articles
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference". An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships". Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today.
In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term, in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable but has no independent effect on the dependent variable, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable.
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from probability + unit. The purpose of the model is to estimate the probability that an observation with particular characteristics will fall into a specific one of the categories; moreover, classifying observations based on their predicted probabilities is a type of binary classification model.
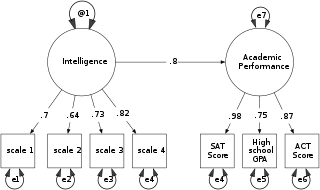
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences.
Takeshi Amemiya is an economist specializing in econometrics and the economy of ancient Greece.
In statistics, a tobit model is any of a class of regression models in which the observed range of the dependent variable is censored in some way. The term was coined by Arthur Goldberger in reference to James Tobin, who developed the model in 1958 to mitigate the problem of zero-inflated data for observations of household expenditure on durable goods. Because Tobin's method can be easily extended to handle truncated and other non-randomly selected samples, some authors adopt a broader definition of the tobit model that includes these cases.
Censored regression models are a class of models in which the dependent variable is censored above or below a certain threshold. A commonly used likelihood-based model to accommodate to a censored sample is the Tobit model, but quantile and nonparametric estimators have also been developed. These and other censored regression models are often confused with truncated regression models. Truncated regression models are used for data where whole observations are missing so that the values for the dependent and the independent variables are unknown. Censored regression models are used for data where only the value for the dependent variable is unknown while the values of the independent variables are still available.
In statistics, model specification is part of the process of building a statistical model: specification consists of selecting an appropriate functional form for the model and choosing which variables to include. For example, given personal income together with years of schooling and on-the-job experience , we might specify a functional relationship as follows:
In statistics, censoring is a condition in which the value of a measurement or observation is only partially known.
The Heckman correction is a statistical technique to correct bias from non-randomly selected samples or otherwise incidentally truncated dependent variables, a pervasive issue in quantitative social sciences when using observational data. Conceptually, this is achieved by explicitly modelling the individual sampling probability of each observation together with the conditional expectation of the dependent variable. The resulting likelihood function is mathematically similar to the tobit model for censored dependent variables, a connection first drawn by James Heckman in 1974. Heckman also developed a two-step control function approach to estimate this model, which avoids the computational burden of having to estimate both equations jointly, albeit at the cost of inefficiency. Heckman received the Nobel Memorial Prize in Economic Sciences in 2000 for his work in this field.
In statistics, truncation results in values that are limited above or below, resulting in a truncated sample. A random variable is said to be truncated from below if, for some threshold value , the exact value of is known for all cases , but unknown for all cases . Similarly, truncation from above means the exact value of is known in cases where , but unknown when .
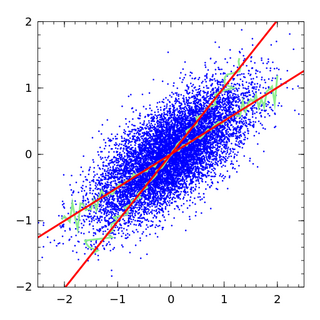
In statistics, errors-in-variables models or measurement error models are regression models that account for measurement errors in the independent variables. In contrast, standard regression models assume that those regressors have been measured exactly, or observed without error; as such, those models account only for errors in the dependent variables, or responses.
A limited dependent variable is a variable whose range of possible values is "restricted in some important way." In econometrics, the term is often used when estimation of the relationship between the limited dependent variable of interest and other variables requires methods that take this restriction into account. For example, this may arise when the variable of interest is constrained to lie between zero and one, as in the case of a probability, or is constrained to be positive, as in the case of wages or hours worked.
In probability theory, the Mills ratio of a continuous random variable is the function

LIMDEP is an econometric and statistical software package with a variety of estimation tools. In addition to the core econometric tools for analysis of cross sections and time series, LIMDEP supports methods for panel data analysis, frontier and efficiency estimation and discrete choice modeling. The package also provides a programming language to allow the user to specify, estimate and analyze models that are not contained in the built in menus of model forms.
Andrew Donald Roy was a British economist who is known for the Roy model of self-selection and income distribution and Roy's safety-first criterion.
Control functions are statistical methods to correct for endogeneity problems by modelling the endogeneity in the error term. The approach thereby differs in important ways from other models that try to account for the same econometric problem. Instrumental variables, for example, attempt to model the endogenous variable X as an often invertible model with respect to a relevant and exogenous instrument Z. Panel analysis uses special data properties to difference out unobserved heterogeneity that is assumed to be fixed over time.
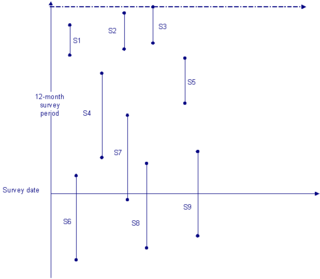
Stock sampling is sampling people in a certain state at the time of the survey. This is in contrast to flow sampling, where the relationship of interest deals with duration or survival analysis. In stock sampling, rather than focusing on transitions within a certain time interval, we only have observations at a certain point in time. This can lead to both left and right censoring. Imposing the same model on data that have been generated under the two different sampling regimes can lead to research reaching fundamentally different conclusions if the joint distribution across the flow and stock samples differ sufficiently.
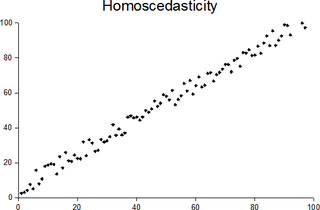
In statistics, a sequence of random variables is homoscedastic if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings homoskedasticity and heteroskedasticity are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient.
References
- ↑ Breen, Richard (1996). Regression Models : Censored, Samples Selected, or Truncated Data. Thousand Oaks: Sage. pp. 2–4. ISBN 0-8039-5710-6.
- ↑ Amemiya, T. (1973). "Regression Analysis When the Dependent Variable is Truncated Normal". Econometrica . 41 (6): 997–1016. doi:10.2307/1914031. JSTOR 1914031.
- ↑ Heckman, James J. (1976). "The Common Structure of Statistical Models of Truncation, Sample Selection, and Limited Dependent Variables and a Simple Estimator for Such Models". Annals of Economic and Social Measurement. 15: 475–492.
- ↑ Heckman, James J. (1979). "Sample Selection Bias as a Specification Error". Econometrica . 47 (1): 153–161. doi:10.2307/1912352. JSTOR 1912352.
- ↑ Lewbel, A.; Linton, O. (2002). "Nonparametric Censored and Truncated Regression" (PDF). Econometrica. 70 (2): 765–779. doi:10.1111/1468-0262.00304. S2CID 120113700.
- ↑ Park, B. U.; Simar, L.; Zelenyuk, V. (2008). "Local Likelihood Estimation of Truncated Regression and its Partial Derivatives: Theory and Application" (PDF). Journal of Econometrics . 146 (1): 185–198. doi:10.1016/j.jeconom.2008.08.007.