| Truncated triakis icosahedron | |
|---|---|
 | |
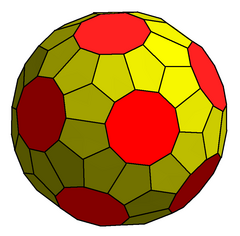| Conway notation | t10kI = dk10tD |
| Faces | 12 decagons 60 pentagons |
| Edges | 210 |
| Vertices | 140 |
| Dual | Decakis truncated dodecahedron |
| Vertex configuration | 12 (5.5.5) 60 (5.5.10) |
| Symmetry group | Ih |
| Properties | convex |
 Net | |
The truncated triakis icosahedron, or more precisely an order-10 truncated triakis icosahedron , is a convex polyhedron with 72 faces: 20 sets of 3 pentagons arranged in an icosahedral arrangement, with 12 decagons in the gaps.
It is constructed from a triakis icosahedron by truncating the order-10 vertices. This creates 12 regular decagon faces, and leaves 60 mirror-symmetric pentagons.
 Triakis icosahedron |
The dual of the truncated triakis icosahedron is called a decakis truncated dodecahedron. It can be seen as a truncated dodecahedron with decagonal pyramids augmented to the faces.
 Truncated dodecahedron |  Decakis truncated dodecahedron |  Net |
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |