Absolute magnitude is a measure of the luminosity of a celestial object on an inverse logarithmic astronomical magnitude scale. An object's absolute magnitude is defined to be equal to the apparent magnitude that the object would have if it were viewed from a distance of exactly 10 parsecs, without extinction of its light due to absorption by interstellar matter and cosmic dust. By hypothetically placing all objects at a standard reference distance from the observer, their luminosities can be directly compared among each other on a magnitude scale. For Solar System bodies that shine in reflected light, a different definition of absolute magnitude (H) is used, based on a standard reference distance of one astronomical unit.

In astronomy, a double planet is a binary satellite system where both objects are planets, or planetary-mass objects, that share an orbital axis external to both planetary bodies.

In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In celestial mechanics, the Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem.

The tidal force is a gravitational effect that stretches a body along the line towards the center of mass of another body due to a gradient in gravitational field from the other body; it is responsible for diverse phenomena, including tides, tidal locking, breaking apart of celestial bodies and formation of ring systems within the Roche limit, and in extreme cases, spaghettification of objects. It arises because the gravitational field exerted on one body by another is not constant across its parts: the nearest side is attracted more strongly than the farthest side. It is this difference that causes a body to get stretched. Thus, the tidal force is also known as the differential force, as well as a secondary effect of the gravitational field.
The Titius–Bode law is a formulaic prediction of spacing between planets in any given solar system. The formula suggests that, extending outward, each planet should be approximately twice as far from the Sun as the one before. The hypothesis correctly anticipated the orbits of Ceres and Uranus, but failed as a predictor of Neptune's orbit. It is named after Johann Daniel Titius and Johann Elert Bode.

Callisto, or Jupiter IV, is the second-largest moon of Jupiter, after Ganymede. In the Solar System it is the third-largest moon after Ganymede and Saturn's largest moon Titan, and as large as the smallest planet Mercury, though only about a third as massive. Callisto is, with a diameter of 4821 km, roughly a third larger than the Moon and orbits Jupiter on average at a distance of 1883000 km, which is about six times further out than the Moon orbiting Earth. It is the outermost of the four large Galilean moons of Jupiter, which were discovered in 1610 with one of the first telescopes, being visible from Earth with common binoculars.

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space.

Ganymede, or Jupiter III, is the largest and most massive natural satellite of Jupiter as well as in the Solar System, being a planetary-mass moon. It is the largest Solar System object without an atmosphere, despite being the only moon of the Solar System with a magnetic field. Like Titan, it is larger than the planet Mercury, but has somewhat less surface gravity than Mercury, Io or the Moon.
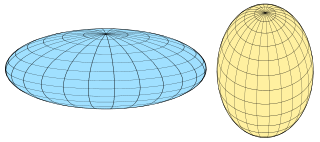
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
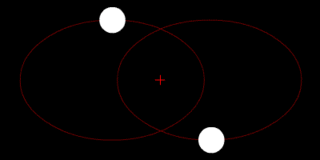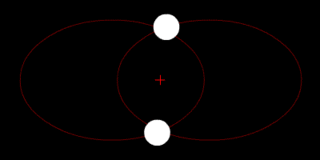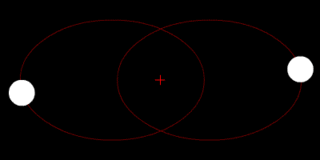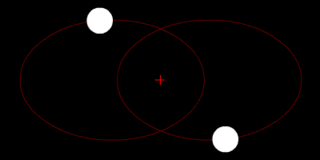
In astronomy, the barycenter is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important concept in fields such as astronomy and astrophysics. The distance from a body's center of mass to the barycenter can be calculated as a two-body problem.

The Gaussian gravitational constant is a parameter used in the orbital mechanics of the Solar System. It relates the orbital period to the orbit's semi-major axis and the mass of the orbiting body in Solar masses.

The Hill sphere of an astronomical body is the region in which it dominates the attraction of satellites. It is sometimes termed the Roche sphere. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.

Orbital decay is a gradual decrease of the distance between two orbiting bodies at their closest approach over many orbital periods. These orbiting bodies can be a planet and its satellite, a star and any object orbiting it, or components of any binary system. If left unchecked, the decay eventually results in termination of the orbit when the smaller object strikes the surface of the primary; or for objects where the primary has an atmosphere, the smaller object burns, explodes, or otherwise breaks up in the larger object's atmosphere; or for objects where the primary is a star, ends with incineration by the star's radiation. Collisions of stellar-mass objects are usually accompanied by effects such as gamma-ray bursts and detectable gravitational waves.

A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region around a celestial body where the primary gravitational influence on an orbiting object is that body. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun. In the patched conic approximation, used in estimating the trajectories of bodies moving between the neighbourhoods of different masses using a two body approximation, ellipses and hyperbolae, the SOI is taken as the boundary where the trajectory switches which mass field it is influenced by.
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.

In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.

Magnetic braking is a theory explaining the loss of stellar angular momentum due to material getting captured by the stellar magnetic field and thrown out at great distance from the surface of the star. It plays an important role in the evolution of binary star systems.



















