First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length and if every other problem that can be solved in polynomial space can be transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE.
In mathematical logic, a universal quantification is a type of quantifier, a logical constant which is interpreted as "given any" or "for all". It expresses that a predicate can be satisfied by every member of a domain of discourse. In other words, it is the predication of a property or relation to every member of the domain. It asserts that a predicate within the scope of a universal quantifier is true of every value of a predicate variable.
In predicate logic, an existential quantification is a type of quantifier, a logical constant which is interpreted as "there exists", "there is at least one", or "for some". It is usually denoted by the logical operator symbol ∃, which, when used together with a predicate variable, is called an existential quantifier ("∃x" or "∃(x)" or "(∃x)"). Existential quantification is distinct from universal quantification ("for all"), which asserts that the property or relation holds for all members of the domain. Some sources use the term existentialization to refer to existential quantification.
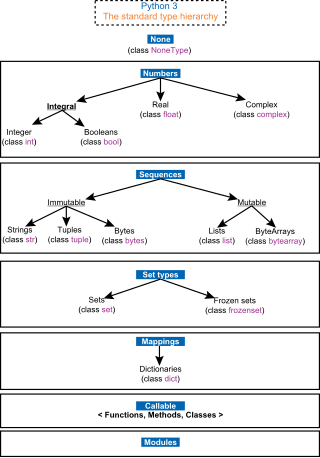
In computer science and computer programming, a data type is a collection or grouping of data values, usually specified by a set of possible values, a set of allowed operations on these values, and/or a representation of these values as machine types. A data type specification in a program constrains the possible values that an expression, such as a variable or a function call, might take. On literal data, it tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans.
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation (symbol) that specifies places in an expression where substitution may take place and is not a parameter of this or any container expression. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. The idea is related to a placeholder, or a wildcard character that stands for an unspecified symbol.
In formal logic and related branches of mathematics, a functional predicate, or function symbol, is a logical symbol that may be applied to an object term to produce another object term. Functional predicates are also sometimes called mappings, but that term has additional meanings in mathematics. In a model, a function symbol will be modelled by a function.
In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a type to every "term". Usually the terms are various constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components.
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.
In mathematical logic, a formula of first-order logic is in Skolem normal form if it is in prenex normal form with only universal first-order quantifiers.
In computational complexity theory, an alternating Turing machine (ATM) is a non-deterministic Turing machine (NTM) with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP. The concept of an ATM was set forth by Chandra and Stockmeyer and independently by Kozen in 1976, with a joint journal publication in 1981.
System F is a typed lambda calculus that introduces, to simply typed lambda calculus, a mechanism of universal quantification over types. System F formalizes parametric polymorphism in programming languages, thus forming a theoretical basis for languages such as Haskell and ML. It was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds.
In computer science and logic, a dependent type is a type whose definition depends on a value. It is an overlapping feature of type theory and type systems. In intuitionistic type theory, dependent types are used to encode logic's quantifiers like "for all" and "there exists". In functional programming languages like Agda, ATS, Coq, F*, Epigram, and Idris, dependent types help reduce bugs by enabling the programmer to assign types that further restrain the set of possible implementations.
In programming languages and type theory, parametric polymorphism allows a single piece of code to be given a "generic" type, using variables in place of actual types, and then instantiated with particular types as needed. Parametrically polymorphic functions and data types are sometimes called generic functions and generic datatypes, respectively, and they form the basis of generic programming.
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics.
The Herbrandization of a logical formula is a construction that is dual to the Skolemization of a formula. Thoralf Skolem had considered the Skolemizations of formulas in prenex form as part of his proof of the Löwenheim–Skolem theorem. Herbrand worked with this dual notion of Herbrandization, generalized to apply to non-prenex formulas as well, in order to prove Herbrand's theorem.
In many programming languages, map is the name of a higher-order function that applies a given function to each element of a collection, e.g. a list or set, returning the results in a collection of the same type. It is often called apply-to-all when considered in functional form.
In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified, using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false. If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT.
A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier in the first order formula expresses that everything in the domain satisfies the property denoted by . On the other hand, the existential quantifier in the formula expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable.
