The thermal conductivity of a material is a measure of its ability to a particular material conduct heat. It is commonly denoted by , , or .
Electrical resistivity is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-meter (Ω⋅m). For example, if a 1 m3 solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves.
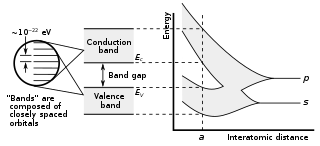
In solid-state physics, a band gap, also called an energy gap, is an energy range in a solid where no electronic states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote a valence electron bound to an atom to become a conduction electron, which is free to move within the crystal lattice and serve as a charge carrier to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there is no generated current due to no net charge carrier mobility. However, if some electrons transfer from the valence band to the conduction band, then current can flow. Therefore, the band gap is a major factor determining the electrical conductivity of a solid. Substances with large band gaps are generally insulators, those with smaller band gaps are semiconductors, while conductors either have very small band gaps or none, because the valence and conduction bands overlap to form a continuous band.

Thermoelectric materials show the thermoelectric effect in a strong or convenient form.
Brillouin scattering, named after Léon Brillouin, refers to the interaction of light with the material waves in a medium. It is mediated by the refractive index dependence on the material properties of the medium; as described in optics, the index of refraction of a transparent material changes under deformation.
In solid-state physics, the electron mobility characterises how quickly an electron can move through a metal or semiconductor when pulled by an electric field. There is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility.
A spin wave is a propagating disturbance in the ordering of a magnetic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are bosonic modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only μeV in keeping with typical Curie points at room temperature and below.
In mesoscopic physics, ballistic conduction is the unimpeded flow of charge carriers, or energy-carrying particles, over relatively long distances in a material. In general, the resistivity of a material exists because an electron, while moving inside a medium, is scattered by impurities, defects, thermal fluctuations of ions in a crystalline solid, or, generally, by any freely-moving atom/molecule composing a gas or liquid. Without scattering, electrons simply obey Newton's second law of motion at non-relativistic speeds.
Phonon drag is an increase in the effective mass of conduction electrons or valence holes due to interactions with the crystal lattice in which the electron moves. As an electron moves past atoms in the lattice its charge distorts or polarizes the nearby lattice. This effect leads to a decrease in the electron mobility, which results in a decreased conductivity. However, as the magnitude of the Seebeck coefficient increases with phonon drag, it may be beneficial in a thermoelectric material for direct energy conversion applications. The magnitude of this effect is typically appreciable only at low temperatures . Phonons are not always in local thermal equilibrium; they move against the thermal gradient. They lose momentum by interacting with electrons and imperfections in the crystal. If the phonon-electron interaction is predominant, the phonons will tend to push the electrons to one end of the material, losing momentum in the process. This contributes to the already present thermoelectric field. This contribution is most important in the temperature region where phonon-electron scattering is predominant. This happens for
Helium atom scattering (HAS) is a surface analysis technique used in materials science. HAS provides information about the surface structure and lattice dynamics of a material by measuring the diffracted atoms from a monochromatic helium beam incident on the sample.

In solid state physics, a surface phonon is the quantum of a lattice vibration mode associated with a solid surface. Similar to the ordinary lattice vibrations in a bulk solid, the nature of surface vibrations depends on details of periodicity and symmetry of a crystal structure. Surface vibrations are however distinct from the bulk vibrations, as they arise from the abrupt termination of a crystal structure at the surface of a solid. Knowledge of surface phonon dispersion gives important information related to the amount of surface relaxation, the existence and distance between an adsorbate and the surface, and information regarding presence, quantity, and type of defects existing on the surface.

In semiconductor physics, the band gap of a semiconductor can be of two basic types, a direct band gap or an indirect band gap. The minimal-energy state in the conduction band and the maximal-energy state in the valence band are each characterized by a certain crystal momentum (k-vector) in the Brillouin zone. If the k-vectors are different, the material has an "indirect gap". The band gap is called "direct" if the crystal momentum of electrons and holes is the same in both the conduction band and the valence band; an electron can directly emit a photon. In an "indirect" gap, a photon cannot be emitted because the electron must pass through an intermediate state and transfer momentum to the crystal lattice.
As the devices continue to shrink further into the sub-100 nm range following the trend predicted by Moore’s law, the topic of thermal properties and transport in such nanoscale devices becomes increasingly important. Display of great potential by nanostructures for thermoelectric applications also motivates the studies of thermal transport in such devices. These fields, however, generate two contradictory demands: high thermal conductivity to deal with heating issues in sub-100 nm devices and low thermal conductivity for thermoelectric applications. These issues can be addressed with phonon engineering, once nanoscale thermal behaviors have been studied and understood.
Interfacial thermal resistance, also known as thermal boundary resistance, or Kapitza resistance, is a measure of resistance to thermal flow at the interface between two materials. While these terms may be used interchangeably, Kapitza resistance technically refers to an atomically perfect, flat interface whereas thermal boundary resistance is a more broad term. This thermal resistance differs from contact resistance because it exists even at atomically perfect interfaces. Owing to differences in electronic and vibrational properties in different materials, when an energy carrier attempts to traverse the interface, it will scatter at the interface. The probability of transmission after scattering will depend on the available energy states on side 1 and side 2 of the interface.
Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by a relaxation rate 1/ which is the inverse of the corresponding relaxation time.
The Monte Carlo method for electron transport is a semiclassical Monte Carlo (MC) approach of modeling semiconductor transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field using classical mechanics. The scattering events and the duration of particle flight is determined through the use of random numbers.
The empty lattice approximation is a theoretical electronic band structure model in which the potential is periodic and weak. One may also consider an empty irregular lattice, in which the potential is not even periodic. The empty lattice approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move through a crystal lattice. The energy of the electrons in the "empty lattice" is the same as the energy of free electrons. The model is useful because it clearly illustrates a number of the sometimes very complex features of energy dispersion relations in solids which are fundamental to all electronic band structures.
For typical three-dimensional metals, the temperature-dependence of the electrical resistivity ρ(T) due to the scattering of electrons by acoustic phonons changes from a high-temperature regime in which ρ ∝ T to a low-temperature regime in which ρ ∝ T5 at a characteristic temperature known as the Debye temperature. For low density electron systems, however, the Fermi surface can be substantially smaller than the size of the Brillouin zone, and only a small fraction of acoustic phonons can scatter off electrons. This results in a new characteristic temperature known as the Bloch–Grüneisen temperature that is lower than the Debye temperature. The Bloch–Grüneisen temperature is defined as 2ħvskF/kB, where ħ is the Planck constant, vs is the velocity of sound, ħkF is the Fermi momentum, and kB is the Boltzmann constant.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.