
In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements . It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
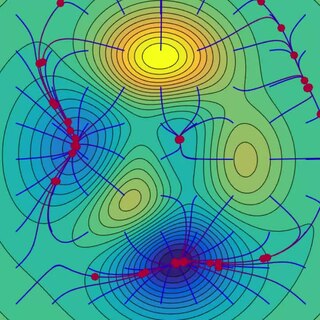
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function.
In mathematics and computing, the Levenberg–Marquardt algorithm, also known as the damped least-squares (DLS) method, is used to solve non-linear least squares problems. These minimization problems arise especially in least squares curve fitting. The LMA interpolates between the Gauss–Newton algorithm (GNA) and the method of gradient descent. The LMA is more robust than the GNA, which means that in many cases it finds a solution even if it starts very far off the final minimum. For well-behaved functions and reasonable starting parameters, the LMA tends to be slower than the GNA. LMA can also be viewed as Gauss–Newton using a trust region approach.

The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. In this sense, the algorithm is also an effective method for solving overdetermined systems of equations. It has the advantage that second derivatives, which can be challenging to compute, are not required.
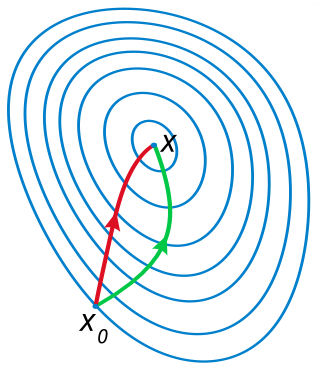
In calculus, Newton's method is an iterative method for finding the roots of a differentiable function , which are solutions to the equation . As such, Newton's method can be applied to the derivative of a twice-differentiable function to find the roots of the derivative, also known as the critical points of . These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function .
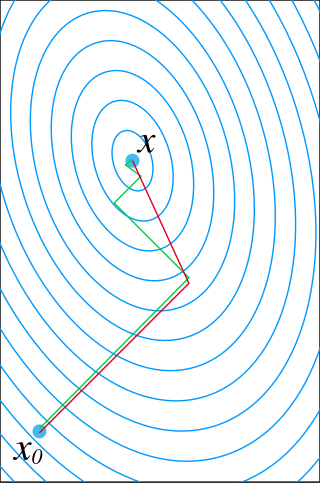
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.
In optimization, line search is a basic iterative approach to find a local minimum of an objective function . It first finds a descent direction along which the objective function will be reduced, and then computes a step size that determines how far should move along that direction. The descent direction can be computed by various methods, such as gradient descent or quasi-Newton method. The step size can be determined either exactly or inexactly.
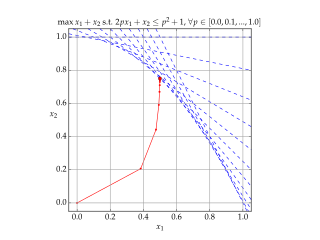
Interior-point methods are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:
In numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is an iterative method for solving unconstrained nonlinear optimization problems. Like the related Davidon–Fletcher–Powell method, BFGS determines the descent direction by preconditioning the gradient with curvature information. It does so by gradually improving an approximation to the Hessian matrix of the loss function, obtained only from gradient evaluations via a generalized secant method.
The Frank–Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization. Also known as the conditional gradient method, reduced gradient algorithm and the convex combination algorithm, the method was originally proposed by Marguerite Frank and Philip Wolfe in 1956. In each iteration, the Frank–Wolfe algorithm considers a linear approximation of the objective function, and moves towards a minimizer of this linear function.
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method.
Limited-memory BFGS is an optimization algorithm in the family of quasi-Newton methods that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) using a limited amount of computer memory. It is a popular algorithm for parameter estimation in machine learning. The algorithm's target problem is to minimize over unconstrained values of the real-vector where is a differentiable scalar function.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
Subgradient methods are convex optimization methods which use subderivatives. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function. When the objective function is differentiable, sub-gradient methods for unconstrained problems use the same search direction as the method of steepest descent.
In numerical analysis, the Schur complement method, named after Issai Schur, is the basic and the earliest version of non-overlapping domain decomposition method, also called iterative substructuring. A finite element problem is split into non-overlapping subdomains, and the unknowns in the interiors of the subdomains are eliminated. The remaining Schur complement system on the unknowns associated with subdomain interfaces is solved by the conjugate gradient method.
An algebraic Riccati equation is a type of nonlinear equation that arises in the context of infinite-horizon optimal control problems in continuous time or discrete time.
In statistics, the backfitting algorithm is a simple iterative procedure used to fit a generalized additive model. It was introduced in 1985 by Leo Breiman and Jerome Friedman along with generalized additive models. In most cases, the backfitting algorithm is equivalent to the Gauss–Seidel method, an algorithm used for solving a certain linear system of equations.
Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is a matrix-free method for finding the largest eigenvalues and the corresponding eigenvectors of a symmetric generalized eigenvalue problem
The conjugate residual method is an iterative numeric method used for solving systems of linear equations. It's a Krylov subspace method very similar to the much more popular conjugate gradient method, with similar construction and convergence properties.

In mathematical optimization, affine scaling is an algorithm for solving linear programming problems. Specifically, it is an interior point method, discovered by Soviet mathematician I. I. Dikin in 1967 and reinvented in the U.S. in the mid-1980s.




























