 | This article needs additional citations for verification .(August 2024) |
In mathematics, Volterra's function, named for Vito Volterra, is a real-valued function V defined on the real line R with the following curious combination of properties:
The function is defined by making use of the Smith–Volterra–Cantor set and an infinite number or "copies" of sections of the function defined by
The construction of V begins by determining the largest value of x in the interval [0, 1/8] for which f′(x) = 0. Once this value (say x0) is determined, extend the function to the right with a constant value of f(x0) up to and including the point 1/8. Once this is done, a mirror image of the function can be created starting at the point 1/4 and extending downward towards 0. This function will be defined to be 0 outside of the interval [0, 1/4]. We then translate this function to the interval [3/8, 5/8] so that the resulting function, which we call f1, is nonzero only on the middle interval of the complement of the Smith–Volterra–Cantor set.
To construct f2, f′ is then considered on the smaller interval [0,1/32], truncated at the last place the derivative is zero, extended, and mirrored the same way as before, and two translated copies of the resulting function are added to f1 to produce the function f2. Volterra's function then results by repeating this procedure for every interval removed in the construction of the Smith–Volterra–Cantor set; in other words, the function V is the limit of the sequence of functions f1, f2, ...
Volterra's function is differentiable everywhere just as f (as defined above) is. One can show that f′(x) = 2x sin(1/x) - cos(1/x) for x ≠ 0, which means that in any neighborhood of zero, there are points where f′ takes values 1 and −1. Thus there are points where V′ takes values 1 and −1 in every neighborhood of each of the endpoints of intervals removed in the construction of the Smith–Volterra–Cantor set S. In fact, V′ is discontinuous at every point of S, even though V itself is differentiable at every point of S, with derivative 0. However, V′ is continuous on each interval removed in the construction of S, so the set of discontinuities of V′ is equal to S.
Since the Smith–Volterra–Cantor set S has positive Lebesgue measure, this means that V′ is discontinuous on a set of positive measure. By Lebesgue's criterion for Riemann integrability, V′ is not Riemann integrable. If one were to repeat the construction of Volterra's function with the ordinary measure-0 Cantor set C in place of the "fat" (positive-measure) Cantor set S, one would obtain a function with many similar properties, but the derivative would then be discontinuous on the measure-0 set C instead of the positive-measure set S, and so the resulting function would have a Riemann integrable derivative.
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function f is a differentiable function F whose derivative is equal to the original function f. This can be stated symbolically as F' = f. The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as F and G.
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883.
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter.
In mathematical analysis, a null set is a Lebesgue measurable set of real numbers that has measure zero. This can be characterized as a set that can be covered by a countable union of intervals of arbitrarily small total length.
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of Göttingen in 1854, but not published in a journal until 1868. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration, or simulated using Monte Carlo integration.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
In calculus and real analysis, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus—differentiation and integration. This relationship is commonly characterized in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the Radon–Nikodym derivative, or density, of a measure. We have the following chains of inclusions for functions over a compact subset of the real line:
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition of this integral was first published in 1894 by Stieltjes. It serves as an instructive and useful precursor of the Lebesgue integral, and an invaluable tool in unifying equivalent forms of statistical theorems that apply to discrete and continuous probability.
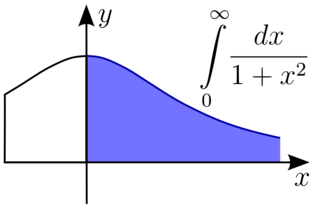
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals, this typically involves unboundedness, either of the set over which the integral is taken or of the integrand, or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral is worked out as if it is improper, the same answer will result.
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes both Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework. The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and conversely every regular Borel measure on the real line is of this kind.
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved or nice. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved.
In mathematics, the Smith–Volterra–Cantor set (SVC), ε-Cantor set, or fat Cantor set is an example of a set of points on the real line that is nowhere dense, yet has positive measure. The Smith–Volterra–Cantor set is named after the mathematicians Henry Smith, Vito Volterra and Georg Cantor. In an 1875 paper, Smith discussed a nowhere-dense set of positive measure on the real line, and Volterra introduced a similar example in 1881. The Cantor set as we know it today followed in 1883. The Smith–Volterra–Cantor set is topologically equivalent to the middle-thirds Cantor set.
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a limit point of its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function.
In mathematics, the Peano–Jordan measure is an extension of the notion of size to shapes more complicated than, for example, a triangle, disk, or parallelepiped.
Thomae's function is a real-valued function of a real variable that can be defined as:
A product integral is any product-based counterpart of the usual sum-based integral of calculus. The product integral was developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations.
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function with the concept of integrating a function. Roughly speaking, the two operations can be thought of as inverses of each other.
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the X axis. The Lebesgue integral, named after French mathematician Henri Lebesgue, is one way to make this concept rigorous and to extend it to more general functions.
In mathematics, the Khinchin integral, also known as the Denjoy–Khinchin integral, generalized Denjoy integral or wide Denjoy integral, is one of a number of definitions of the integral of a function. It is a generalization of the Riemann and Lebesgue integrals. It is named after Aleksandr Khinchin and Arnaud Denjoy, but is not to be confused with the (narrow) Denjoy integral.
