Wavelet for multidimensional signals analysis

Last updated

Wavelets are often used to analyse piece-wise smooth signals. [1] Wavelet coefficients can efficiently represent a signal which has led to data compression algorithms using wavelets. [2] Wavelet analysis is extended for multidimensional signal processing as well. This article introduces a few methods for wavelet synthesis and analysis for multidimensional signals. There also occur challenges such as directivity in multidimensional case.

Contents

Multidimensional separable discrete wavelet transform (DWT)

The discrete wavelet transform is extended to the multidimensional case using the tensor product of well known 1-D wavelets. In 2-D for example, the tensor product space for 2-D is decomposed into four tensor product vector spaces [3] as

(φ(x) ⨁ ψ(x)) ⊗ (φ(y) ⨁ ψ(y)) = { φ(x)φ(y), φ(x)ψ(y), ψ(x)φ(y), ψ(x)ψ(y) }

This leads to the concept of multidimensional separable DWT similar in principle to the multidimensional DFT.

φ(x)φ(y) gives the approximation coefficients and other subbands:

φ(x)ψ(y) low-high (LH) subband,

ψ(x)φ(y) high-low (HL) subband,

ψ(x)ψ(y) high-high (HH) subband,

give detail coefficients.

Implementation of multidimensional separable DWT

Wavelet coefficients can be computed by passing the signal to be decomposed though a series of filters. In the case of 1-D, there are two filters at every level-one low pass for approximation and one high pass for the details. In the multidimensional case, the number of filters at each level depends on the number of tensor product vector spaces. For M-D, 2M filters are necessary at every level. Each of these is called a subband. The subband with all low pass (LLL...) gives the approximation coefficients and all the rest give the detail coefficients at that level. For example, for M=3 and a signal of size N1 × N2 × N3 , a separable DWT can be implemented as follows:

The figure depicts 3-D separable DWT procedure by applying 1-D DWT for each dimension and splitting the data into chunks to obtain wavelets for different subbands Wiki figures mod.001.png
The figure depicts 3-D separable DWT procedure by applying 1-D DWT for each dimension and splitting the data into chunks to obtain wavelets for different subbands

Applying the 1-D DWT analysis filterbank in dimension N1, it is now split into two chunks of size N1⁄2 × N2 × N3. Applying 1-D DWT in N2 dimension, each of these chunks is split into two more chunks of N1⁄2 × N2⁄2 × N3. This repeated in 3-D gives a total of 8 chunks of size N1⁄2 × N2⁄2 × N3⁄2. [4]

The figure shows the 3-D analysis filterbank for 3-D separable DWT Filterbank mod try 2.001.png
The figure shows the 3-D analysis filterbank for 3-D separable DWT

Disadvantages of M-D separable DWT

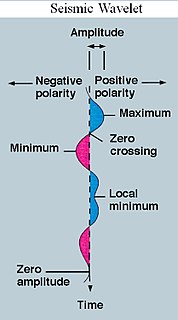
The wavelets generated by the separable DWT procedure are highly shift variant. A small shift in the input signal changes the wavelet coefficients to a large extent. Also, these wavelets are almost equal in their magnitude in all directions and thus do not reflect the orientation or directivity that could be present in the multidimensional signal. For example, there could be an edge discontinuity in an image or an object moving smoothly along a straight line in the space-time 4D dimension. A separable DWT does not fully capture the same. In order to overcome these difficulties, a method of wavelet transform called Complex wavelet transform (CWT) was developed.

Multidimensional complex wavelet transform

Similar to the 1-D complex wavelet transform, [5] tensor products of complex wavelets are considered to produce complex wavelets for multidimensional signal analysis. With further analysis it is seen that these complex wavelets are oriented. [6] This sort of orientation helps to resolve the directional ambiguity of the signal.

Implementation of multidimensional (M-D) dual tree CWT

Dual tree CWT in 1-D uses 2 real DWTs, where the first one gives the real part of CWT and the second DWT gives the imaginary part of the CWT. M-D dual tree CWT is analyzed in terms of tensor products. However, it is possible to implement M-D CWTs efficiently using separable M-D DWTs and considering sum and difference of subbands obtained. Additionally, these wavelets tend to be oriented in specific directions.

Two types of oriented M-D CWTs can be implemented. Considering only the real part of the tensor product of wavelets, real coefficients are obtained. All wavelets are oriented in different directions. This is 2m times as expansive where m is the dimensions.

If both real and imaginary parts of the tensor products of complex wavelets are considered, complex oriented dual tree CWT which is 2 times more expansive than real oriented dual tree CWT is obtained. So there are two wavelets oriented in each of the directions. Although implementing complex oriented dual tree structure takes more resources, it is used in order to ensure an approximate shift invariance property that a complex analytical wavelet can provide in 1-D. In the 1-D case, it is required that the real part of the wavelet and the imaginary part are Hilbert transform pairs for the wavelet to be analytical and to exhibit shift invariance. Similarly in the M-D case, the real and imaginary parts of tensor products are made to be approximate Hilbert transform pairs in order to be analytic and shift invariant. [6] [7]

Consider an example for 2-D dual tree real oriented CWT:

Let ψ(x) and ψ(y) be complex wavelets:

ψ(x) = ψ(x)h + j ψ(x)g and ψ(y) = ψ(y)h + j ψ(y)g.

ψ(x,y) = [ψ(x)h + j ψ(x)g][ ψ(y)h + j ψ(y)g] = ψ(x)hψ(y)h - ψ(x)gψ(x)g + j [ψ(x)hψ(y)g - ψ(x)hψ(x)g]

The support of the Fourier spectrum of the wavelet above resides in the first quadrant. When just the real part is considered, Real(ψ(x,y)) = ψ(x)hψ(y)h - ψ(x)gψ(x)g has support on opposite quadrants (see (a) in figure). Both ψ(x)hψ(y)h and ψ(x)gψ(y)g correspond to the HH subband of two different separable 2-D DWTs. This wavelet is oriented at -45o.

Similarly, by considering ψ2(x,y) = ψ(x)ψ(y)*, a wavelet oriented at 45o is obtained. To obtain 4 more oriented real wavelets, φ(x)ψ(y), ψ(x)φ(y), φ(x)ψ(y)* and ψ(x)φ(y)* are considered.

The implementation of complex oriented dual tree structure is done as follows: Two separable 2-D DWTs are implemented in parallel using the filterbank structure as in the previous section. Then, the appropriate sum and difference of different subbands (LL, LH, HL, HH) give oriented wavelets, a total of 6 in all.

The figure shows the Fourier support of all 6 oriented wavelets obtained by a 2-D real oriented dual tree CWT Wavelet orientation.jpg
The figure shows the Fourier support of all 6 oriented wavelets obtained by a 2-D real oriented dual tree CWT

Similarly, in 3-D, 4 separable 3-D DWTs in parallel are needed and a total of 28 oriented wavelets are obtained.

Disadvantage of M-D CWT

Although the M-D CWT provides one with oriented wavelets, these orientations are only appropriate to represent the orientation along the (m-1)th dimension of a signal with m dimensions. When singularities in manifold [8] of lower dimensions are considered, such as a bee moving in a straight line in the 4-D space-time, oriented wavelets that are smooth in the direction of the manifold and change rapidly in the direction normal to it are needed. A new transform, Hypercomplex Wavelet transform was developed in order to address this issue.

Hypercomplex wavelet transform

The dual tree hypercomplex wavelet transform (HWT) developed in [9] consists of a standard DWT tensor and 2m -1 wavelets obtained from combining the 1-D Hilbert transform of these wavelets along the n-coordinates. In particular a 2-D HWT consists of the standard 2-D separable DWT tensor and three additional components:

Hx {ψ(x)hψ(y)h} = ψ(x)gψ(y)h

Hy {ψ(x)hψ(y)h} = ψ(x)hψ(y)g

Hx Hy {ψ(x)hψ(y)h} = ψ(x)gψ(y)g

For the 2-D case, this is named dual tree quaternion wavelet transform (QWT). [10] The total redundancy in M-D is 2m tight frame.

Directional hypercomplex wavelet transform

The hypercomplex transform described above serves as a building block to construct the directional hypercomplex wavelet transform (DHWT). A linear combination of the wavelets obtained using the hypercomplex transform give a wavelet oriented in a particular direction. For the 2-D DHWT, it is seen that these linear combinations correspond to the exact 2-D dual tree CWT case. For 3-D, the DHWT can be considered in two dimensions, one DHWT for n = 1 and another for n = 2. For n = 2, n = m-1, so, as in the 2-D case, this corresponds to 3-D dual tree CWT. But the case of n = 1 gives rise to a new DHWT transform. The combination of 3-D HWT wavelets is done in a manner to ensure that the resultant wavelet is lowpass along 1-D and bandpass along 2-D. In, [9] this was used to detect line singularities in 3-D space.

Challenges ahead

The wavelet transforms for multidimensional signals are often computationally challenging which is the case with most multidimensional signals. Also, the methods of CWT and DHWT are redundant even though they offer directivity and shift invariance.

Related Research Articles

Wavelet

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one recorded by a seismograph or heart monitor. Generally, wavelets are intentionally crafted to have specific properties that make them useful for signal processing.

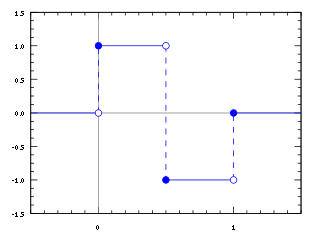
Haar wavelet

In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example.

A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies. The DCT, first proposed by Nasir Ahmed in 1972, is a widely used transformation technique in signal processing and data compression. It is used in most digital media, including digital images, digital video, digital audio, digital television, digital radio, and speech coding. DCTs are also important to numerous other applications in science and engineering, such as digital signal processing, telecommunication devices, reducing network bandwidth usage, and spectral methods for the numerical solution of partial differential equations.

Continuous wavelet transform

In mathematics, the continuous wavelet transform (CWT) is a formal tool that provides an overcomplete representation of a signal by letting the translation and scale parameter of the wavelets vary continuously.

Discrete wavelet transform transform in numerical harmonic analysis

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.

Filter bank

In signal processing, a filter bank is an array of bandpass filters that separates the input signal into multiple components, each one carrying a single frequency sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.

The Fast Wavelet Transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain. This algorithm was introduced in 1989 by Stéphane Mallat.

Embedded Zerotrees of Wavelet transforms (EZW) is a lossy image compression algorithm. At low bit rates, i.e. high compression ratios, most of the coefficients produced by a subband transform will be zero, or very close to zero. This occurs because "real world" images tend to contain mostly low frequency information. However where high frequency information does occur this is particularly important in terms of human perception of the image quality, and thus must be represented accurately in any high quality coding scheme.

A multiresolution analysis (MRA) or multiscale approximation (MSA) is the design method of most of the practically relevant discrete wavelet transforms (DWT) and the justification for the algorithm of the fast wavelet transform (FWT). It was introduced in this context in 1988/89 by Stephane Mallat and Yves Meyer and has predecessors in the microlocal analysis in the theory of differential equations and the pyramid methods of image processing as introduced in 1981/83 by Peter J. Burt, Edward H. Adelson and James L. Crowley.

Originally known as Optimal Subband Tree Structuring (SB-TS) also called Wavelet Packet Decomposition (WPD) (sometimes known as just Wavelet Packets or Subband Tree) is a wavelet transform where the discrete-time (sampled) signal is passed through more filters than the discrete wavelet transform (DWT).


The Stationary wavelet transform (SWT) is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of in the th level of the algorithm. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input – so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as "algorithme à trous" in French which refers to inserting zeros in the filters. It was introduced by Holschneider et al.

The complex wavelet transform (CWT) is a complex-valued extension to the standard discrete wavelet transform (DWT). It is a two-dimensional wavelet transform which provides multiresolution, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of shift-invariance in its magnitude, which was investigated in. However, a drawback to this transform is that it exhibits redundancy compared to a separable (DWT).

Wavelet transform

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.

An orthogonal wavelet is a wavelet whose associated wavelet transform is orthogonal. That is, the inverse wavelet transform is the adjoint of the wavelet transform. If this condition is weakened one may end up with biorthogonal wavelets.

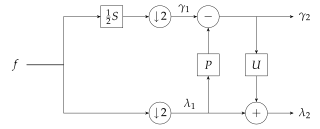
Lifting scheme technique for wavelet analysis

The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.

Geophysical survey is the systematic collection of geophysical data for spatial studies. Detection and analysis of the geophysical signals forms the core of Geophysical signal processing. The magnetic and gravitational fields emanating from the Earth's interior hold essential information concerning seismic activities and the internal structure. Hence, detection and analysis of the electric and Magnetic fields is very crucial. As the Electromagnetic and gravitational waves are multi-dimensional signals, all the 1-D transformation techniques can be extended for the analysis of these signals as well. Hence this article also discusses multi-dimensional signal processing techniques.

Contourlets form a multiresolution directional tight frame designed to efficiently approximate images made of smooth regions separated by smooth boundaries. The contourlet transform has a fast implementation based on a Laplacian pyramid decomposition followed by directional filterbanks applied on each bandpass subband.

Power spectral estimation forms the basis for distinguishing and tracking signals in the presence of noise and extracting information from available data. One dimensional signals are expressed in terms of a single domain while multidimensional signals are represented in wave vector and frequency spectrum. Therefore, spectral estimation in the case of multidimensional signals gets a bit tricky.

This article provides a short survey of the concepts, principles and applications of Multirate Filter Banks and Multidimensional Directional Filter Banks.

References

  1. ↑ Mallat, Stéphane (2008). A Wavelet Tour of Signal Processing. Academic Press.
  2. ↑ Devore, R.A.; Jawerth, B.; Lucier, B.J. (1991). "Data compression using wavelets: Error, smoothness and quantization". [1991] Proceedings. Data Compression Conference. pp. 186–195. doi:10.1109/DCC.1991.213386. ISBN   978-0-8186-9202-4.
  3. ↑ Kugarajah, Tharmarajah; Zhang, Qinghua (November 1995). "Multidimensional wavelet frames". IEEE Transactions on Neural Networks. 6 (6): 1552–1556. doi:10.1109/72.471353. hdl: 1903/5619 . PMID   18263450.
  4. ↑ Cheng-Wu, Po; Gee-Chen, Liang (7 August 2002). "An efficient architecture for two-dimensional discrete wavelet transform". IEEE Transactions on Circuits and Systems for Video Technology. 11 (4): 536–545. doi:10.1109/76.915359.
  5. ↑ Kingsbury, Nick (2001). "Complex Wavelets for Shift Invariant Analysis and Filtering of Signals". Applied and Computational Harmonic Analysis. 10 (3): 234–253. doi: 10.1006/acha.2000.0343 .
  6. 1 2 Selesnick, Ivan; Baraniuk, Richard; Kingsbury, Nick (2005). "The Dual-Tree Complex Wavelet Transform". IEEE Signal Processing Magazine. 22 (6): 123–151. Bibcode:2005ISPM...22..123S. doi:10.1109/MSP.2005.1550194. hdl: 1911/20355 .
  7. ↑ Selesnick, I.W. (June 2001). "Hilbert transform pairs of wavelet bases". IEEE Signal Processing Letters. 8 (6): 170–173. Bibcode:2001ISPL....8..170S. CiteSeerX   10.1.1.139.5369 . doi:10.1109/97.923042.
  8. ↑ Boothby, W (2003). An Introduction to Differentiable Manifolds and Riemannian Geometry. San Diego: Academic.
  9. 1 2 Wai Lam Chan; Hyeokho Choi; Baraniuk, R.G. (2004). "Directional hypercomplex wavelets for multidimensional signal analysis and processing". 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing. 3. pp. iii–996–9. doi:10.1109/ICASSP.2004.1326715. hdl:1911/19796. ISBN   0-7803-8484-9.
  10. ↑ Lam Chan, Wai; Choi, Hyeokho; Baraniuk, Richard (2008). "Coherent Multiscale Image Processing Using Dual-Tree Quaternion Wavelets". IEEE Transactions on Image Processing. 17 (7): 1069–1082. Bibcode:2008ITIP...17.1069C. doi:10.1109/TIP.2008.924282. PMID   18586616.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.