In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

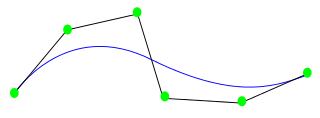
A Bézier curve is a parametric curve used in computer graphics and related fields. The curve, which is related to the Bernstein polynomial, is named after Pierre Bézier, who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation. Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter.

In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.
A Bézier triangle is a special type of Bézier surface, which is created by interpolation of control points.

In mathematics, a projective space can be thought of as the set of lines through the origin of a vector space V. The cases when V = R2 and V = R3 are the real projective line and the real projective plane, respectively, where R denotes the field of real numbers, R2 denotes ordered pairs of real numbers, and R3 denotes ordered triplets of real numbers.

Algebraic varieties are the central objects of study in algebraic geometry. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
Non-uniform rational basis spline (NURBS) is a mathematical model commonly used in computer graphics for generating and representing curves and surfaces. It offers great flexibility and precision for handling both analytic and modeled shapes. NURBS are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE) and are part of numerous industry wide standards, such as IGES, STEP, ACIS, and PHIGS. NURBS tools are also found in various 3D modeling and animation software packages.
In mathematics, the Riemann–Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, describes the relationship of the Euler characteristics of two surfaces when one is a ramified covering of the other. It therefore connects ramification with algebraic topology, in this case. It is a prototype result for many others, and is often applied in the theory of Riemann surfaces and algebraic curves.
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class. They are in some sense the opposite of surfaces of general type, which have ample canonical class.
In mathematics, a dessin d'enfant is a type of graph embedding used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers. The name of these embeddings is French for a "child's drawing"; its plural is either dessins d'enfant, "child's drawings", or dessins d'enfants, "children's drawings".

In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.
In mathematics, the rational normal curve is a smooth, rational curve C of degree n in projective n-space Pn. It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n = 2 it is the flat conic Z0Z2 = Z2
1, and for n = 3 it is the twisted cubic. The term "normal" refers to projective normality, not normal schemes. The intersection of the rational normal curve with an affine space is called the moment curve.
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the field of real numbers, a rational point is more commonly called a real point.
In algebraic geometry, a Fano variety, introduced by Gino Fano in, is a complete variety X whose anticanonical bundle KX* is ample. In this definition, one could assume that X is smooth over a field, but the minimal model program has also led to the study of Fano varieties with various types of singularities, such as terminal or klt singularities.

In mathematics, a polynomial lemniscate or polynomial level curve is a plane algebraic curve of degree 2n, constructed from a polynomial p with complex coefficients of degree n.
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space, refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials. The basic theory of Hilbert schemes was developed by Alexander Grothendieck (1961). Hironaka's example shows that non-projective varieties need not have Hilbert schemes.
In algebraic geometry, an infinitely near point of an algebraic surface S is a point on a surface obtained from S by repeatedly blowing up points. Infinitely near points of algebraic surfaces were introduced by Max Noether (1876).
Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, and/or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.
In algebraic geometry, a variety over a field k is ruled if it is birational to the product of the projective line with some variety over k. A variety is uniruled if it is covered by a family of rational curves. The concept arose from the ruled surfaces of 19th-century geometry, meaning surfaces in affine space or projective space which are covered by lines. Uniruled varieties can be considered to be relatively simple among all varieties, although there are many of them.
The curved point-normal triangle, in short PN triangle, is an interpolation algorithm to retrieve a cubic Bézier triangle from the vertex coordinates of a regular flat triangle and normal vectors. The PN triangle retains the vertices of the flat triangle as well as the corresponding normals. It was first introduced by A. Vlachos et al. in 2001 and is primarily used in the field of computer graphics. The usage of the PN triangle enables the visualization of triangle based surfaces in a smoother shape at low cost in terms of rendering complexity and time.