In mathematics, the classic Möbius inversion formula is a relation between pairs of arithmetic functions, each defined from the other by sums over divisors. It was introduced into number theory in 1832 by August Ferdinand Möbius.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.

In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.
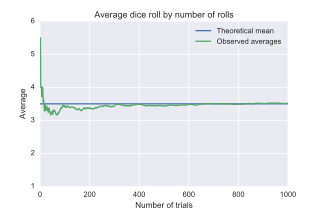
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed.
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant. It is named after the Russian mathematician Andrey Markov, although it appeared earlier in the work of Pafnuty Chebyshev, and many sources, especially in analysis, refer to it as Chebyshev's inequality or Bienaymé's inequality.
In mathematics, the Radon–Nikodym theorem is a result in measure theory that expresses the relationship between two measures defined on the same measurable space. A measure is a set function that assigns a consistent magnitude to the measurable subsets of a measurable space. Examples of a measure include area and volume, where the subsets are sets of points; or the probability of an event, which is a subset of possible outcomes within a wider probability space.
In mathematics, concentration of measure is a principle that is applied in measure theory, probability and combinatorics, and has consequences for other fields such as Banach space theory. Informally, it states that "A random variable that depends in a Lipschitz way on many independent variables is essentially constant".
In complex analysis, the Phragmén–Lindelöf principle, first formulated by Lars Edvard Phragmén (1863–1937) and Ernst Leonard Lindelöf (1870–1946) in 1908, is a technique which employs an auxiliary, parameterized function to prove the boundedness of a holomorphic function on an unbounded domain when an additional condition constraining the growth of on is given. It is a generalization of the maximum modulus principle, which is only applicable to bounded domains.
In measure theory, an area of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is also named Severini–Egoroff theorem or Severini–Egorov theorem, after Carlo Severini, an Italian mathematician, and Dmitri Egorov, a Russian physicist and geometer, who published independent proofs respectively in 1910 and 1911.
In mathematics, and particularly in the field of complex analysis, the Hadamard factorization theorem asserts that every entire function with finite order can be represented as a product involving its zeroes and an exponential of a polynomial. It is named for Jacques Hadamard.
Convergence in measure is either of two distinct mathematical concepts both of which generalize the concept of convergence in probability.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.
In probability theory, Lindeberg's condition is a sufficient condition for the central limit theorem (CLT) to hold for a sequence of independent random variables. Unlike the classical CLT, which requires that the random variables in question have finite variance and be both independent and identically distributed, Lindeberg's CLT only requires that they have finite variance, satisfy Lindeberg's condition, and be independent. It is named after the Finnish mathematician Jarl Waldemar Lindeberg.
In mathematics, in the field of complex analysis, a Nevanlinna function is a complex function which is an analytic function on the open upper half-plane and has non-negative imaginary part. A Nevanlinna function maps the upper half-plane to itself or to a real constant, but is not necessarily injective or surjective. Functions with this property are sometimes also known as Herglotz, Pick or R functions.
Stochastic portfolio theory (SPT) is a mathematical theory for analyzing stock market structure and portfolio behavior introduced by E. Robert Fernholz in 2002. It is descriptive as opposed to normative, and is consistent with the observed behavior of actual markets. Normative assumptions, which serve as a basis for earlier theories like modern portfolio theory (MPT) and the capital asset pricing model (CAPM), are absent from SPT.
Generalized relative entropy is a measure of dissimilarity between two quantum states. It is a "one-shot" analogue of quantum relative entropy and shares many properties of the latter quantity.
In probability theory, Kolmogorov's two-series theorem is a result about the convergence of random series. It follows from Kolmogorov's inequality and is used in one proof of the strong law of large numbers.
Adding controlled noise from predetermined distributions is a way of designing differentially private mechanisms. This technique is useful for designing private mechanisms for real-valued functions on sensitive data. Some commonly used distributions for adding noise include Laplace and Gaussian distributions.
The two-dimensional critical Ising model is the critical limit of the Ising model in two dimensions. It is a two-dimensional conformal field theory whose symmetry algebra is the Virasoro algebra with the central charge . Correlation functions of the spin and energy operators are described by the minimal model. While the minimal model has been exactly solved, see also, e.g., the article on Ising critical exponents, the solution does not cover other observables such as connectivities of clusters.


































